
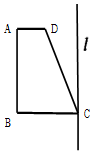
 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=1,BC=2,∠DCB=60°,在平面ABCD内过点C作l⊥CB,将梯形ABCD以l为轴旋转一周
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=1,BC=2,∠DCB=60°,在平面ABCD内过点C作l⊥CB,将梯形ABCD以l为轴旋转一周分析 (1)旋转后形成的几何体为圆柱中挖去一个倒放的与圆柱等高的圆锥,由此能求出旋转体的体积.
(2)先求出圆柱的侧面积、底面积,再求出圆锥的侧面积、底面积和旋转体上底面的面积,由此能求出结果.
解答  解:(1)旋转后形成的几何体为圆柱中挖去一个倒放的与圆柱等高的圆锥,
解:(1)旋转后形成的几何体为圆柱中挖去一个倒放的与圆柱等高的圆锥,
$CD=\frac{BC-AD}{cos60°}=2,AB=CDsin60°=\sqrt{3}$,
∴小圆锥的半径r=BC-AD=1,
$圆柱的体积{V_1}=π{R^2}h=π×{2^2}×\sqrt{3}=4\sqrt{3}π$,
$圆锥的体积{V_2}=\frac{1}{3}π{r^2}h=\frac{1}{3}π×{1^2}×\sqrt{3}=\frac{{\sqrt{3}}}{3}π$,
∴$旋转体的体积V={V_1}-{V_2}=4\sqrt{3}π-\frac{{\sqrt{3}}}{3}π=\frac{{11\sqrt{3}}}{3}π$…(5分)
$(2)圆柱的侧面积{S_1}=2πRl=2π×2×\sqrt{3}=4\sqrt{3}π$
圆锥的侧面积S2=πrl=π×1×2=2π,
$圆柱的底面积{S_3}=π{R^2}=π×{2^2}=4π$,
$圆锥的底面积{S_4}=π{r^2}=π×{1^2}=π$,
旋转体上底面的面积S5=S3-S4=3π,
∴$旋转体的表面积={S_1}+{S_2}+{S_3}+{S_5}=(4\sqrt{3}+9)π$.…(12分)
点评 本题考查旋转体的体积和表面积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


科目:高中数学 来源: 题型:选择题
| 气温X(0C) | 18 | 13 | 10 | -1 |
| 用电量y | 24 | 34 | 38 | 64 |
| A. | 60 | B. | 58 | C. | 62 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其东北方向与它相距32海里的B处有一外国船只,且D岛位于海监船正东28$\sqrt{2}$海里处.
如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其东北方向与它相距32海里的B处有一外国船只,且D岛位于海监船正东28$\sqrt{2}$海里处.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com