
 如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其东北方向与它相距32海里的B处有一外国船只,且D岛位于海监船正东28$\sqrt{2}$海里处.
如图,我海监船在D岛海域例行维权巡航,某时刻航行至A处,此时测得其东北方向与它相距32海里的B处有一外国船只,且D岛位于海监船正东28$\sqrt{2}$海里处.分析 (1)△ABD中,由余弦定理求解得BD的值,即为所求.
(2)过点B作BC⊥AD于点C,以点D为圆心、以24为半径的圆交BC于点E,连结AE,DE,
则由题意可得,我海监船在点C处拦截住外国船只时,我海监船的速度
v取得最小值.求得AC=BC、CD的值,再求得CE、BE、AE的值,可得外国船只沿正南方向航行的时间,从而求得我海监船的速度v,由sin∠EAC=$\frac{CE}{AE}$求得∠EAC 的值,进而可求海监船的航向.
解答 (本题满分为12分)
解:(1)依题意,在△ABD中,∠DAB=45°,
由余弦定理得$D{B^2}=A{D^2}+A{B^2}-2AD•AB•cos{45^0}={({28\sqrt{2}})^2}+{32^2}-2×28\sqrt{2}×32×\frac{{\sqrt{2}}}{2}=800$,
∴$DB=20\sqrt{2}$.…(4分)
即此时该外国船只与D岛的距离为$20\sqrt{2}$海里.…(5分)
(2)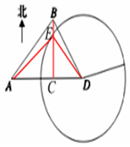 过点B作BC⊥AD于点C,
过点B作BC⊥AD于点C,
在Rt△ABC中,$AC=BC=16\sqrt{2}$,
∴$CD=AD-AC=12\sqrt{2}$,…(6分)
以D为圆心,24为半径的圆交BC于点E,连结AE,DE,
在Rt△DEC中,$CE=\sqrt{E{D^2}-C{D^2}}=12\sqrt{2}$,
∴$BE=4\sqrt{2}$,…(7分)
又$AE=\sqrt{A{C^2}+C{E^2}}=20\sqrt{2}$,
∴$sin∠EAC=\frac{CE}{AE}=\frac{3}{5}⇒∠EAC≈{36^0}52'$,…(9分)
外国船只到达点E的时间$t=\frac{BE}{8}=\frac{{\sqrt{2}}}{2}$(小时),
∴海监船的速度$v≥\frac{AE}{t}=40$(海里/小时),…(11分)
故海监船的航向为北偏东900-36052'=53008',速度的最小值为40海里/小时.…(12分)
点评 本题主要考查解三角形的实际应用,直角三角形中的边角关系、余弦定理的应用,考查了数形结合思想,属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
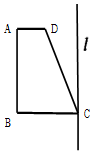 如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=1,BC=2,∠DCB=60°,在平面ABCD内过点C作l⊥CB,将梯形ABCD以l为轴旋转一周
如图,梯形ABCD中,AD∥BC,∠ABC=90°,AD=1,BC=2,∠DCB=60°,在平面ABCD内过点C作l⊥CB,将梯形ABCD以l为轴旋转一周查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{(-5)^{2}}$=-5 | B. | $\root{4}{{a}^{4}}$=a | C. | $\sqrt{{7}^{2}}$=7 | D. | $\root{3}{(-π)^{3}}$=π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com