练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    15．函数f（x）=$\frac{{x}^{2}-2x+9}{x}$（x＜0）最大值为-8．

    分析 f（x）=$\frac{{x}^{2}-2x+9}{x}$=$\frac{9}{x}+x-2=-[（-x）+\frac{9}{-x}]-2≤-2\sqrt{-x•\frac{9}{-x}}-2\\;\\;=-8$，再利用基本不等式即可．

    解答 解：∵x＜0，∴f（x）=$\frac{{x}^{2}-2x+9}{x}$=$\frac{9}{x}+x-2=-[（-x）+\frac{9}{-x}]-2≤-2\sqrt{-x•\frac{9}{-x}}-2\\;\\;=-8$=-8
    故答案为：-8

    点评 本题考查了应用基本不等式求最值，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    5．已知函数y=2${\;}^{-{x^2}+ax-1}}$在[-1，1]上是增函数，则a的取值范围是{a|a≥2}．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    6．集合A={x|-3＜x＜7}，B={x|t+1＜x＜2t-1}，若B⊆A，则实数t的取值范围是（-∞，4]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

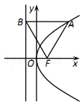    3．如图，抛物线的顶点在坐标原点，焦点为F，过抛物线上一点A（3，y）作准线l作垂线，垂直为B，若|AB|=|BF|，则抛物线的标准方程是（　　）
    A．y2=$\frac{1}{2}$xB．y2=xC．y2=2xD．y2=4x

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知函数f（x）=$\overrightarrow m•\overrightarrow n$，其中$\overrightarrow m=（sinωx+cosωx，\sqrt{3}cosωx）$，$\overrightarrow n=（cosωx-sinωx，2sinωx）$，其中ω＞0，若f（x）相邻两对称轴间的距离为$\frac{π}{2}$．
    （Ⅰ） 求函数f（x）的单调递增区间；
    （Ⅱ）在△ABC中，a，b，c分别为角A、B、C的对边，a=$\sqrt{3}$，b+c=3，f（A）=1，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知函数f（x）=$\left\{\begin{array}{l}-{（x-1）^2}，（{x＜1}）\\（3-a）x+4a，（{x≥1}）\end{array}$为增函数，则实数a的取值范围是（　　）
    A．-1≤a＜3B．a＜3C．a＞3或a≤-1D．-1＜a＜3

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．图中的阴影表示的集合中是（　　）
    A．A∩∁UBB．B∩∁UAC．∁U（A∩B）D．∁U（A∪B）

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．某单位为了了解用电量y（度）与气温X（0C）之间的关系，随机统计了某4天的用电量与当天气温，并作了如下的对照表：由表中数据，得回归直线方程$\hat y$=$\hat bx$+$\hat a$，若$\hat b$=-2，则$\hat a$=（　　）
    气温X（0C）181310-1
    用电量y24343864
    A．60B．58C．62D．64

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    5．如图，我海监船在D岛海域例行维权巡航，某时刻航行至A处，此时测得其东北方向与它相距32海里的B处有一外国船只，且D岛位于海监船正东28$\sqrt{2}$海里处．
    （1）求此时该外国船只与D岛的距离；
    （2）观测中发现，此外国船只正以每小时8海里的速度沿正南方向航行，为了将该船拦截在离D岛24海里处，不让其进入D岛24海里内的海域，试确定海监船的航向，并求其速度的最小值．（参考数据：sin36°52'≈0.6，sin53°08'≈0.8）

    查看答案和解析>>

    同步练习册答案