
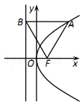
 如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )
如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )| A. | y2=$\frac{1}{2}$x | B. | y2=x | C. | y2=2x | D. | y2=4x |
分析 根据抛物线的基本概念与正三角形的性质,利用解直角三角形算出|BF|=2p,由AB⊥y轴,可得3+$\frac{p}{2}$=2p,求出p,即可求出抛物线的标准方程.
解答 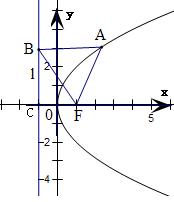 解:由题意,△ABF为等边三角形,设直线l交x轴于点C,
解:由题意,△ABF为等边三角形,设直线l交x轴于点C,
∵AB⊥l,l⊥x轴,
∴AB∥x轴,可得∠BFC=∠ABF=60°,
Rt△BCF中,|CF|=|BF|cos60°=p,解得|BF|=2p,
由AB⊥y轴,可得3+$\frac{p}{2}$=2p,
∴p=2,
∴抛物线的标准方程是y2=4x.
故选:D.
点评 本题给出抛物线中的正三角形满足的条件,求抛物线的标准方程,着重考查了抛物线的基本概念、正三角形的性质与解直角三角形等知识,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | (-∞,0)上是增函数 | B. | (0,+∞)上是增函数 | C. | (-∞,3)上是增函数 | D. | (3,+∞)上是增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
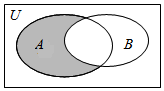 设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )
设全集U=R,A={x|x(x-2)<0},B={x|y=$\sqrt{1-x}$},则图中阴影部分表示的集合为( )| A. | {x|0<x≤1} | B. | {x|1<x<2} | C. | {x|x≤1} | D. | {x|1≤x<2} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
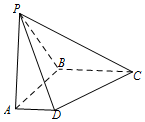 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com