
分析 根据题意将已知的等式转化为向量的数量积运算,由向量的数量积运算、完全平方公式化简,再由基本不等式列出关于“λ+μ”的不等式,即可求出λ+μ的最大值.
解答 解:∵<$\overrightarrow{OA}$,$\overrightarrow{OB}$>=120°,正数λ,μ满足$\overrightarrow{OC}$=λ$\overrightarrow{OA}$+μ$\overrightarrow{OB}$,
且向量$\overrightarrow{OA}$,$\overrightarrow{OB}$,$\overrightarrow{OC}$的模长都为1,
∴${\overrightarrow{OC}}^{2}=(λ\overrightarrow{OA}+μ\overrightarrow{OB})^{2}$=${λ}^{2}{\overrightarrow{OA}}^{2}+2λμ\overrightarrow{OA}•\overrightarrow{OB}+{μ}^{2}{\overrightarrow{OB}}^{2}$
则1=λ2-λμ+μ2=(λ+μ)2-3λμ,
即3λμ=(λ+μ)2-1,
∵λ>0,μ>0,∴$λμ≤(\frac{λ+μ}{2})^{2}$,当且仅当λ=μ时取等号,
代入上式可得,${(λ+μ)}^{2}-1≤3{(\frac{λ+μ}{2})}^{2}$,
化简可得,(λ+μ)2≤4,则0<λ+μ≤2,
∴λ+μ的最大值是2,
故答案为:2.
点评 本题考查了向量的数量积运算,以及基本不等式在求最值中的应用,考查转化思想,化简、变形能力.


科目:高中数学 来源: 题型:选择题
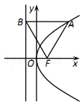 如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )
如图,抛物线的顶点在坐标原点,焦点为F,过抛物线上一点A(3,y)作准线l作垂线,垂直为B,若|AB|=|BF|,则抛物线的标准方程是( )| A. | y2=$\frac{1}{2}$x | B. | y2=x | C. | y2=2x | D. | y2=4x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1≤a<3 | B. | a<3 | C. | a>3或a≤-1 | D. | -1<a<3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 气温X(0C) | 18 | 13 | 10 | -1 |
| 用电量y | 24 | 34 | 38 | 64 |
| A. | 60 | B. | 58 | C. | 62 | D. | 64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (-∞,0) | C. | (1,+∞) | D. | (0,2) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com