
| A. | ②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
分析 求出直线所过定点坐标,可判断①;求出圆被y轴截得的弦长,可判断②;分析直线所过定义与圆的位置关系,可判断③;求出满足条件的直线方程,可判断④.
解答 解:将l的方程整理为(x+y-4)+m(2x+y-7)=0,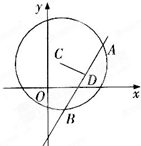
由x+y-4=0,且2x+y-7=0,
解得x=3,y=1,
则无论m为何值,直线l过定点D(3,1).
故①正确;
令x=0,
则(y-2)2=24,
解得:y=2±2$\sqrt{6}$,
故圆C被y轴截得的弦长为 4$\sqrt{6}$;
故②正确;
因为(3-1)2+(1-2)2=5<25,
则点D在圆C的内部,直线l与圆C相交.
故③正确
圆心C(1,2),半径为5,|CD|=$\sqrt{5}$,
当截得的弦长最小时,l⊥CD,由于kCD=-$\frac{1}{2}$,
则l的斜率为2,此时直线的方程为:y-1=2(x-3),即2x-y-5=0,
故④正确;
故选:D
点评 本题以命题的真假判断与应用为载体,考查了直线与圆的位置关系,难度中档.


科目:高中数学 来源: 题型:选择题
| A. | -2009 | B. | 2009 | C. | -2010 | D. | 2010 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
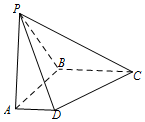 如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.
如图,在底面是直角梯形的四棱锥P-ABCD中,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=3,梯形上底AD=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
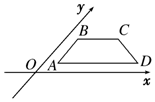 用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )
用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )| A. | 4 cm2 | B. | 4$\sqrt{2}$ cm2 | C. | 8 cm2 | D. | 8$\sqrt{2}$ cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com