
分析 (Ⅰ)当n=1时,a1=s1=1,当n≥2时,${a}_{n}={s}_{n}-{s}_{n-1}=\frac{{n}^{2}+3n}{4}-\frac{(n-1)^{2}+3(n-1)}{4}$=$\frac{n+1}{2}$;
(Ⅱ)由(Ⅰ)得${a}_{n}=\frac{n+1}{2},{b}_{n}={2}^{n+1}$;$\frac{1}{{b}_{1}}+\frac{1}{{b}_{2}}+\frac{1}{{b}_{3}}+…\frac{1}{{b}_{n}}$=$\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}+…+\frac{1}{{2}^{n+1}}$=$\frac{\frac{1}{4}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}=\frac{1}{2}(1-\frac{1}{{2}^{n}})$
解答 解:(Ⅰ)当n=1时,a1=s1=1,
当n≥2时,${a}_{n}={s}_{n}-{s}_{n-1}=\frac{{n}^{2}+3n}{4}-\frac{(n-1)^{2}+3(n-1)}{4}$=$\frac{n+1}{2}$
经检验${a}_{1}也符合{a}_{n}=\frac{n+1}{2}$,∴${a}_{n}=\frac{n+1}{2}…(n∈{N}^{+})$.
(Ⅱ)由(Ⅰ)得${a}_{n}=\frac{n+1}{2}∴{b}_{n}={2}^{n+1}$;
$\frac{1}{{b}_{1}}+\frac{1}{{b}_{2}}+\frac{1}{{b}_{3}}+…\frac{1}{{b}_{n}}$=$\frac{1}{{2}^{2}}+\frac{1}{{2}^{3}}+\frac{1}{{2}^{4}}+…+\frac{1}{{2}^{n+1}}$=$\frac{\frac{1}{4}(1-\frac{1}{{2}^{n}})}{1-\frac{1}{2}}=\frac{1}{2}(1-\frac{1}{{2}^{n}})$
点评 本题考查了等比数列的通项及求和,及公式an=sn-sn-1的应用,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ②③ | B. | ①③④ | C. | ①②④ | D. | ①②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{3}$ | B. | $2\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $2\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
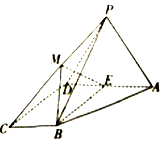 如图,四棱锥P-ABCD的底面为直角梯形,AD∥BC,AD=2BC=2,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为正三角形,M是棱PC上的一点(异于端点).
如图,四棱锥P-ABCD的底面为直角梯形,AD∥BC,AD=2BC=2,BC⊥DC,∠BAD=60°,平面PAD⊥底面ABCD,E为AD的中点,△PAD为正三角形,M是棱PC上的一点(异于端点).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com