
分析 (1)求出函数的导数,通过讨论a的范围,求出函数的单调区间即可;
(2)利用函数零点的性质,结合函数单调性和导数之间的关系,构造函数,利用导数进行转化即可证明不等式.
解答 解:(1)由题可知,g'(x)=e(2-a)x+xe(2-a)x(2-a)=e(2-a)x[(2-a)x+1].
①当a<2时,令g'(x)≥0,则(2-a)x+1≥0,∴$x≥\frac{1}{a-2}$,令g'(x)<0,则(2-a)x+1<0,∴$x<\frac{1}{a-2}$.
②当a=2时,g'(x)>0.
③当a>2时,令g'(x)≥0,则(2-a)x+1≥0,∴$x≤\frac{1}{a-2}$,令g'(x)<0,则(2-a)x+1<0,∴$x>\frac{1}{a-2}$,
综上,①当a<2时,y=g(x)在$({-∞,\frac{1}{a-2}})$上单调递减,在$[{\frac{1}{a-2},+∞})$上单调递增;
②当a=2时,y=g(x)在R上单调递增;
③当a>2时,y=g(x)在$({-∞,\frac{1}{a-2}})$上单调递增,在$[{\frac{1}{a-2},+∞})$上单调递减.
(2)因为f(x)=ln(xe(2-a)x)-ax2=lnx+(2-a)x-ax2(x>0),
所以$f'(x)=\frac{1}{x}+({2-a})-2ax=-\frac{{({2x+1})({ax-1})}}{x}$,
当a≤0时,f'(x)>0,y=f(x)在(0,+∞)上单调递增,与x轴不可能有两个交点,故a>0.
当a>0时,令f'(x)≥0,则$0<x≤\frac{1}{a}$;令f'(x)<0,则$x>\frac{1}{a}$.
故y=f(x)在$({0,\frac{1}{a}}]$上单调递增,在$({\frac{1}{a},+∞})$上单调递减.
不妨设A(x1,m),B(x2,m),且$0<{x_1}<\frac{1}{a}<{x_2}$.
要证f'(x0)<0,需证ax0-1>0,即证${x_0}>\frac{1}{a}⇒{x_1}+{x_2}>\frac{2}{a}⇒{x_2}>\frac{2}{a}-{x_1}⇒f({x_2})<f({\frac{2}{a}-{x_1}})$,
又f(x1)=f(x2),
所以只需证$f({x_1})<f({\frac{2}{a}-{x_1}})$.即证:当$0<x<\frac{1}{a}$时,$f({\frac{2}{a}-x})-f(x)>0$.
设$F(x)=f({\frac{2}{a}-x})-f(x)=ln({2-ax})-ln({ax})+2ax-2$,
则$F'(x)=-\frac{2}{2-ax}-\frac{1}{x}+2a=-\frac{{2{{({ax-1})}^2}}}{{x({2-ax})}}<0$,
所以$F(x)=f({\frac{2}{a}-x})-f(x)$在$({0,\frac{1}{a}})$上单调递减,
又$F({\frac{1}{a}})=f({\frac{2}{a}-\frac{1}{a}})-f({\frac{1}{a}})=0$,
故$F(x)=f({\frac{2}{a}-x})-f(x)>0$.
点评 本题主要考查函数单调性和导数之间的关系和应用,综合性较强,运算量较大,属于中档题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:高中数学 来源: 题型:选择题
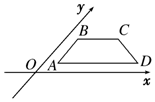 用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )
用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )| A. | 4 cm2 | B. | 4$\sqrt{2}$ cm2 | C. | 8 cm2 | D. | 8$\sqrt{2}$ cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | $\frac{3}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com