
分析 (1)利用三角函数恒等变换的应用化简可得解析式f(x)=2sin(2x-$\frac{π}{3}$),利用周期公式可求最小正周期,由-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{3}$≤$\frac{π}{2}$+2kπ,可得解得f(x)的单调增区间.
(2)由$0≤x≤\frac{π}{2}$,可得$-\frac{π}{3}≤2x-\frac{π}{3}≤\frac{2π}{3}$,利用正弦函数的图象和性质可求函数f(x)的最大值和最小值.
解答 (本题满分为12分)
解:(1)∵f(x)=sin2x-$\sqrt{3}$cos2x=2sin(2x-$\frac{π}{3}$),…(2分)
∴T=π.…(3分)
由-$\frac{π}{2}$+2kπ≤2x-$\frac{π}{3}$≤$\frac{π}{2}$+2kπ,可得解得:-$\frac{π}{12}$+kπ≤x≤$\frac{5π}{12}$+kπ,k∈Z,
∴f(x)的单调增区间为:$[{-\frac{π}{12}+kπ,\frac{5π}{12}+kπ}]$(k∈z).…(6分)
(2)∵$0≤x≤\frac{π}{2}$,
∴$-\frac{π}{3}≤2x-\frac{π}{3}≤\frac{2π}{3}$,可得:$-\frac{{\sqrt{3}}}{2}≤sin({2x-\frac{π}{3}})≤1$,
∴$f{(x)_{max}}=2,f{(x)_{min}}=-\sqrt{3}$.…(12分)
点评 本题主要考查了三角函数恒等变换的应用,三角函数的周期公式的应用,考查了正弦函数的图象和性质,考查了计算能力和数形结合思想,属于中档题.


 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案科目:高中数学 来源: 题型:解答题
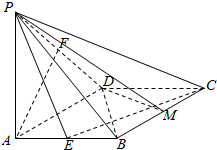 如图,在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB、PD的中点.
如图,在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB、PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -4 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
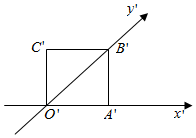 如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )
如图,正方形O′A′C′B′的边长为1cm,它是水平放置的一个平面图形的直观图,则它的原图形面积和直观图面积之比是( )| A. | 2$\sqrt{2}$ | B. | $\frac{\sqrt{2}}{4}$ | C. | 2(1+$\sqrt{3}$) | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\sqrt{3}$ | D. | $\frac{\sqrt{3}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -e | B. | e | C. | 2e | D. | 3e |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com