
某水晶制品厂去年的年产量为10万件,每件水晶产品的销售价格为100元,固定成本为80元.从今年起,工厂投入100万元科技成本,并计划以后每年比上一年多投入100万元科技成本,预计产量每年递增1万件,每件水晶产品的固定成本 与科技成本的投入次数
与科技成本的投入次数 的关系是
的关系是 .若水晶产品的销售价格不变,第
.若水晶产品的销售价格不变,第 次投入后的年利润为
次投入后的年利润为 万元.
万元.
( 1 )求 的表达式;
的表达式;
( 2 )问从今年算起第几年利润最高?最高利润为多少万元?
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=|x+1|,g(x)=2|x|+a.
(1)当a=0时,解不等式f(x)≥g(x);
(2)若任意x∈R,f(x)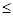 g(x)恒成立,求实数a的取值范围.
g(x)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
函数 和
和 的图像如图所示,设两函数的图像交于点
的图像如图所示,设两函数的图像交于点 .
.
(1)请指出示意图中曲线 分别对应哪一个函数?
分别对应哪一个函数?
(2) ,且
,且 ,指出
,指出 的值,并说明理由;
的值,并说明理由;
(3)结合函数图像示意图,请把
四个数按从小到大的顺序排列.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,问小正方形的边长为多少时,盒子容积最大,并求出此最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示是某水产养殖厂的养殖大网箱的平面图,四周的实线为网衣,为避免混养,
(1)若大网箱的面积为108平方米,每个小网箱的横边 、纵边
、纵边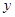 设计为多少米时,才能使围成的网箱中筛网的总长度最小?
设计为多少米时,才能使围成的网箱中筛网的总长度最小?
(2)若大网箱的面积为160平方米,网衣的造价为112元/米,筛网的造价为96元/米,且大网箱的长与宽都不超过15米,则小网箱的横、纵边分别为多少米时,可使总造价最低?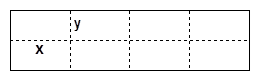
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设某市现有从事第二产业人员100万人,平均每人每年创造产值a万元(a为正常数),现在决定从中分流x万人去加强第三产业。分流后,继续从事第二产业的人员平均每人每年创造产值可增加2x%(0<x<100)。而分流出的从事第三产业的人员,平均每人每年可创造产值1.2a万元。
(1)若要保证第二产业的产值不减少,求x的取值范围;
(2)在(1)的条件下,问应分流出多少人,才能使该市第二、三产业的总产值增加最多?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
提高大桥的车辆通行能力可改善整个城市的交通状况.一般情况下,大桥上的车流
速度v(单位:千米/小时)是车流密度x(单位:辆/千米)的函数.当车流密度不超过50辆/千米时,车流速度为30千米/小时.研究表明:当50<x≤200时,车流速度v与车流密度x满足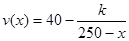 .当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时.
(Ⅰ)当0<x≤200时,求函数v(x)的表达式;
(Ⅱ)当车流密度x为多大时,车流量(单位时间内通过桥上观测点的车辆数,单位:
辆/小时)f(x)=x·v(x)可以达到最大,并求出最大值.(精确到个位,参考数据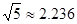 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com