练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    6．已知cosα+cosβ=$\frac{1}{2}$，则cos$\frac{α+β}{2}$cos$\frac{α-β}{2}$的值为$\frac{1}{4}$．

    分析 用三角函数的积化和差公式化简所求后代入已知即可求值．

    解答 解：∵cosα+cosβ=$\frac{1}{2}$，
    ∴cos$\frac{α+β}{2}$cos$\frac{α-β}{2}$=$\frac{1}{2}$[cos（$\frac{α+β}{2}$-$\frac{α-β}{2}$）+cos（$\frac{α+β}{2}$+$\frac{α-β}{2}$）]=$\frac{1}{2}$（cosα+cosβ）=$\frac{1}{2}×\frac{1}{2}$=$\frac{1}{4}$．
    故答案为：$\frac{1}{4}$．

    点评 本题主要考查了三角函数的积化和差公式在三角函数求值中的应用，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    16．在抛物线y=x2+ax-5（a≠0）上取横坐标为x1=-4，x2=2的两点A，B，过这两点引一条割线，抛物线在点Q平行于该割线的一条切线同时与圆5x2+5y2=36相切
    （1）求切点Q的横坐标       
    （2）求切线和坐标轴所围三角形面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

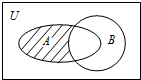    17．已知全集U=R，集合$A=\{\;x|\;{（\frac{1}{2}）^x}≤1\;\}$，B={x|x2-6x+8≤0}，则图中阴影部分所表示的集合为（　　）
    A．{x|x≤0}B．{x|2≤x≤4}C．{x|0＜x≤2或x≥4}D．{x|0≤x＜2或x＞4}

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．在等比数列{an}中，a3=1，a7=4，则a5=2．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．若y=f（x2），则y′等于（　　）
    A．2xf′（x2）B．2xf′（x）C．4x2f（x）D．f′（x2）

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．$\underset{lim}{x→∞}$（1+x）${\;}^{\frac{1}{x}}$=1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    18．求下列函数的导数：
    （1）y=$\frac{1}{{x}^{4}}$；
    （2）y=$\root{5}{{x}^{3}}$；
    （3）y=1-2sin2$\frac{x}{2}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．利用定积分的几何意义求下列定积分：
    （1）${∫}_{-4}^{4}\sqrt{16-{x}^{2}}dx$
    （2）${∫}_{0}^{5}\sqrt{25-{x}^{2}}dx$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=（x-1）ex，g（x）=lnx，其中e是自然对数的底数．
    （1）求函数f（x）的极值；
    （2）求函数h（x）=f（x）+e|g（x）-a|（a为常数）的单调区间．

    查看答案和解析>>

    同步练习册答案