
分析 因为直接受A感染的人至少是B,而C、D二人也有可能是由A感染的,设B、C、D直接受A感染为事件B、C、D,则B、C、D是相互独立的.利用概率公式求解即可.
解答 解:根据题意得出:因为直接受A感染的人至少是B,而C、D二人也有可能是由A感染的,
p(B)=1,设B、C、D直接受A感染为事件B、C、D,
则B、C、D是相互独立的,
并且P(B)=1,P(C)=$\frac{1}{2}$,P(D)=$\frac{1}{3}$,
表明除了B外,C、D二人中恰有1人是由A感染的,
∴P(C$\overline{D}$+$\overline{C}$D)=P(C)P($\overline{D}$)+P($\overline{C}$)P(D)=$\frac{1}{2}×\frac{2}{3}$$+\frac{1}{2}×\frac{1}{3}=\frac{1}{2}$,
∴B、C、D中直接受A传染的人数为2的概率为$\frac{1}{2}$.
故答案为:$\frac{1}{2}$
点评 本题考查了概率的求解,独立事件的求解,学生的阅读能力,是中档题,解题时要认真审题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
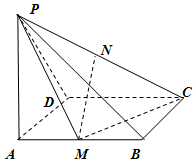 如图,PA⊥矩形ABCD所在的平面,PA=AD,且M,N分别是AB,PC的中点.
如图,PA⊥矩形ABCD所在的平面,PA=AD,且M,N分别是AB,PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{8}$ | B. | $\frac{1}{7}$ | C. | $\frac{1}{3}$ | D. | $\frac{8}{15}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{6}$ | C. | $\frac{{3\root{3}{9}}}{4}$ | D. | $\frac{{3\root{3}{36}}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
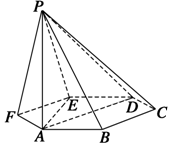 如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的序号是④.
如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论正确的序号是④.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | $2+4\sqrt{2}$ | C. | $4+2\sqrt{5}$ | D. | $2\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{5}{18}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30 | B. | 31 | C. | 32 | D. | 34 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com