已知函数f(x)=kx+m,数列{an},{bn}满足:当x∈[a1,b1]时,f(x)的值域是[a2,b2];当x∈[a2,b2]时,f(x)的值域是[a3,b3],…,当x∈[an-1,bn-1](n∈N,且n≥2)时,f(x)的值域是{an,bn},其中k,m为常数,a1=0,b1=1.
(1)若k=1,m=2,求a2,b2以及数列{an}与{bn}的通项;
(2)若k=2,且数列{bn}是等比数列,求m的值;
(3)(附加题:5分,记入总分,但总分不超过150分)若k>0,设{an}与{bn}的前n项和分别为Sn和Tn,求-.
【答案】
分析:(1)因为k=1,m=2,所以f(x)=x+2在R上是增函数,从而可知数列{a
n}与{b
n}是公差为2的等差数列,故可求a
2,b
2以及数列{a
n}与{b
n}的通项;
(2)因为k=2,所以f(x)=2x+m在R上是增函数,所以b
n+1=2b
n+m,n∈N
+,根据{b
n}是等比数列,所以b
n≠0
于是
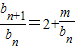
(是常数),从而m=0或{b
n}是常数列,故可求m的值;
(3)因为k>0,所以f(x)=kx+m在R上是增函数,可得{b
n-a
n}是以b
1-a
1为首项,k为公比的等比数列
所以
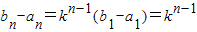
,故T
n-S
n=(b
1-a
1)+(b
2-a
2)+…+(b
n-a
n)=
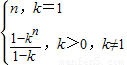
,从而可求(T
1+T
2+••+T
n)-(S
1+S
2+••+S
n)的值.
解答:解:(1)因为k=1,m=2,所以f(x)=x+2在R上是增函数,
所以a
2=a
1+2=2,b
2=b
1+2=3,
a
n=a
n-1+2,b
n=b
n-1+2(n∈N
+,且n≥2)
所以数列{a
n}与{b
n}是公差为2的等差数列.
又a
1=0,b
1=1,所以a
n=2(n-1),b
n=2n-1.
(2)因为k=2,所以f(x)=2x+m在R上是增函数,
所以b
n+1=2b
n+m,n∈N
+,
又因为{b
n}是等比数列,所以b
n≠0
于是
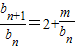
(是常数)
所以m=0或{b
n}是常数列,
又b
1=1,所以若{b
n}是常数列,则必有b
2=2b
1+m=2+m=1,即m=-1
综上,m=0或m=-1.
(附加题)(3)因为k>0,所以f(x)=kx+m在R上是增函数,
所以a
n=ka
n-1+m,b
n=kb
n-1+m(n∈N
+,且n≥2)
两式相减得b
n-a
n=k(b
n-1-a
n-1)
即{b
n-a
n}是以b
1-a
1为首项,k为公比的等比数列
所以
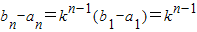
∴T
n-S
n=(b
1-a
1)+(b
2-a
2)+…+(b
n-a
n)=
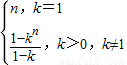
∴(T
1+T
2+••+T
n)-(S
1+S
2+••+S
n)=(T
1-S
1)+(T
2-S
2)+…+(T
n-S
n)
=
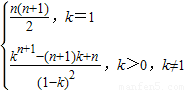
.
点评:本题以函数为载体,考查等差数列与等比数列的通项,考查数列的求和,将数列转化为等差数列与等比数列是解题的关键.

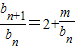 (是常数),从而m=0或{bn}是常数列,故可求m的值;
(是常数),从而m=0或{bn}是常数列,故可求m的值;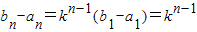 ,故Tn-Sn=(b1-a1)+(b2-a2)+…+(bn-an)=
,故Tn-Sn=(b1-a1)+(b2-a2)+…+(bn-an)=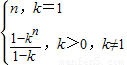
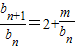 (是常数)
(是常数)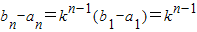
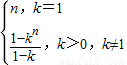
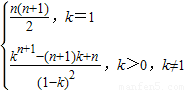 .
.

 口算能手系列答案
口算能手系列答案