
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 (1)根据椭圆的第二定义可知$\frac{A{F}_{1}}{{d}_{2}}=\frac{A{F}_{2}}{{d}_{1}}=e$;
(2),分别取点A为椭圆的四个顶点验证,符合题意;
(3),由$\frac{{|A{F_1}|}}{{|A{F_2}|}}=\frac{{|{F_1}M|}}{{|M{F_2}|}}$,得AM为∠F1AF2的角平分线,得直线AM⊥l;
(4),当四边形的四个顶点为椭圆的定点时和分布在四个象限都可以.
解答 解:对于(1)根据椭圆的第二定义可知$\frac{A{F}_{1}}{{d}_{2}}=\frac{A{F}_{2}}{{d}_{1}}=e$,故错;
对于(2),分别取点A为椭圆的四个顶点验证,符合题意,故正确;
对于(3),A为椭圆上且不在坐标轴上的任一点,过A的椭圆切线为l,则∠F1AF2的角平分线垂直l,∵$\frac{{|A{F_1}|}}{{|A{F_2}|}}=\frac{{|{F_1}M|}}{{|M{F_2}|}}$,∴AM为∠F1AF2的角平分线,故正确;
对于(4),当四边形的四个顶点为椭圆的定点时和分布在四个象限都可以,故错.
故答案为:B.
点评 本题考查了椭圆的性质,比较难,但可以采用特殊情况验证法判定,属于压轴题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{4}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
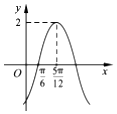 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)的解析式为( )| A. | $f(x)=2sin({x-\frac{π}{6}})$ | B. | $f(x)=2sin({2x-\frac{π}{3}})$ | C. | $f(x)=2sin({x+\frac{π}{12}})$ | D. | $f(x)=2sin({2x-\frac{π}{6}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )
我校教育处连续30天对同学们的着装进行检查,着装不合格的人数为如图所示的茎叶图,则中位数,众数,极差分别是( )| A. | 44,45,56 | B. | 44,43,57 | C. | 44,43,56 | D. | 45,43,57 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 56 | B. | 68 | C. | 78 | D. | 82 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com