
分析 (1)先根据向量的平行得到n(Sn+1-2Sn)=2Sn,继而得到$\frac{{S}_{{\;}_{n+1}}}{n+1}$=2•$\frac{{S}_{n}}{n}$,问题得以证明,
(2)由(1)可得以${S_n}=n•{2^{n-1}}$,由错位相减法即可求出数列{Sn}的前n项和Tn.
解答 证明:(1)$\overrightarrow a=({S_{n+1}}-2{S_n},{S_n})$,$\overrightarrow b=(2,n)$,$\overrightarrow a∥\overrightarrow b$.
∴n(Sn+1-2Sn)=2Sn,
∴$\frac{{S}_{{\;}_{n+1}}}{n+1}$=2•$\frac{{S}_{n}}{n}$,
∴a1=1,
∴$\frac{{S}_{1}}{1}$=1,
∴数列$\{\frac{S_n}{n}\}$是以1为首项,以2为公比的等比数列
(2)由(1)知$\frac{S_n}{n}={2^{n-1}}(n∈{N^+})$,
∴${S_n}=n•{2^{n-1}}$,
∴Tn=1×20+2×21+3×22+…+n•2n-1,
∴2Tn=1×21+2×22+…+(n-1)•2n-1+n•2n,
由错位相减得-Tn=1+21+22+…+2n-1-n•2n=$\frac{1(1-{2}^{n})}{1-2}$-n•2n=2n-1-n•2n=(1-n)2n-1,
∴Tn=(n-1)2n+1
点评 本题考查了向量的平行和等比数列的定义和错位相减法求和,属于中档题.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 12 | B. | 24 | C. | $4\sqrt{3}$ | D. | $8\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a>b>c | B. | b>a>c | C. | c>a>b | D. | b>c>a |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
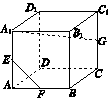 如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )
如图所示,在正方体ABCD-A1B1C1D1中,AA1,AB,CC1的中点分别为E,F,G,则EF与A1G所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com