
分析 (1)设线段AB的中点为M(a,b),由此列出方程组求出a、b的值;根据圆C的圆心C与点M的距离与半径r的大小即可证明直线L与圆C恒有两个交点;
(2)由直线L被圆C截得的弦最短时直线L⊥MC,求出L的斜率,写出直线方程,再求出最小弦长.
解答 解:(1)证明:设线段AB的中点为M(a,b),
依题意$\left\{\begin{array}{l}a-4b-1=0\\ \frac{|2a-5b+9|}{{\sqrt{29}}}=\frac{|2a-5b-7|}{{\sqrt{29}}}\end{array}\right.$,…(2分)
解得a=-3,b=-1;…(3分)
∵圆C:(x+4)2+(y-1)2=25圆心为C(-4,1),半径r=5;…(4分)
且|MC|=$\sqrt{{[-4-(-3)]}^{2}{+[1-(-1)]}^{2}}$=$\sqrt{5}$<r,
∴直线L与圆C恒有两个交点; …(6分)
(2)∵当直线L被圆C截得的弦最短时直线L⊥MC,…(8分)
∴kL=-$\frac{1}{{k}_{MC}}$=-$\frac{-4-(-3)}{1-(-1)}$=$\frac{1}{2}$,
则直线L为$y+1=\frac{1}{2}(x+3)$,
即x-2y+1=0,…(10分)
最小弦长为|EF|=$2\sqrt{{r^2}-|MC{|^2}}=4\sqrt{5}$.…(12分)
点评 本题考查了直线与圆的位置关系的应用问题,也考查了直线垂直以及两点间的距离公式的应用问题,是综合性题目.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
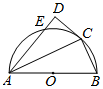 已知AB为半圆O的直径,C为半圆上一点,CD是半圆的切线,AC平分∠BAD,AD交半圆于点E.
已知AB为半圆O的直径,C为半圆上一点,CD是半圆的切线,AC平分∠BAD,AD交半圆于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1 | C. | x2+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{3}$+y2=1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com