
分析 (1)根据平面向量的加减运算法则,求出向量$\overrightarrow{{A}_{7}{A}_{8}}$,再求模长即可;
(2)根据平面向量的加法运算法则,求出$\overrightarrow{O{A_n}}$、$\overrightarrow{O{B_n}}$的坐标表示.
解答 解:(1)∵$\overrightarrow{{{A}_{n-1}A}_{n}}$=2$\overrightarrow{{{A}_{n}A}_{n+1}}$,
∴$\overrightarrow{{A}_{1}{A}_{2}}$=2$\overrightarrow{{A}_{2}{A}_{3}}$=22$\overrightarrow{{A}_{3}{A}_{4}}$=23$\overrightarrow{{{A}_{4}A}_{5}}$=…=26$\overrightarrow{{{A}_{7}A}_{8}}$;
又∵$\overrightarrow{{A}_{1}{A}_{2}}$=5$\overrightarrow{j}$-$\overrightarrow{j}$=4$\overrightarrow{j}$,
∴$\overrightarrow{{A}_{7}{A}_{8}}$=$\frac{1}{16}$$\overrightarrow{j}$,
∴|$\overrightarrow{{A}_{7}{A}_{8}}$|=$\frac{1}{16}$;…(4分)
(2)n=1时,$\overrightarrow{O{A_n}}$=$\overrightarrow{{OA}_{1}}$=$\overrightarrow{j}$,
n≥2时,$\overrightarrow{O{A_n}}$=$\overrightarrow{O{A_1}}+$$\overrightarrow{{A_1}{A_2}}+\overrightarrow{{A_2}{A_3}}+…$$\overrightarrow{{A_{n-1}}{A_n}}$
=$\overrightarrow{j}$+[4$\overrightarrow{j}$+2$\overrightarrow{j}$+…+4•${(\frac{1}{2})}^{n-2}$•$\overrightarrow{j}$]
=$\overrightarrow{j}$+$\frac{4[1{-(\frac{1}{2})}^{n-1}]}{1-\frac{1}{2}}$$\overrightarrow{j}$
=(9-24-n)$\overrightarrow{j}$,
从而,$\overrightarrow{O{A_n}}$=(0,9-24-n);…(8分)
$\overrightarrow{O{B_n}}$=$\overrightarrow{O{B_1}}+$$\overrightarrow{{B_1}{B_2}}+\overrightarrow{{B_2}{B_3}}+…$$\overrightarrow{{B_{n-1}}{B_n}}$
=$(3\overrightarrow i+3\overrightarrow j)+(n-1)(2\overrightarrow i+2\overrightarrow j)$
=$(2n+1)\overrightarrow i+(2n+1)\overrightarrow j$;
从而,$\overrightarrow{O{B_n}}$=(2n+1,2n+1).…(12分)
点评 本题考查了平面向量加减运算以及向量的坐标运算问题,也考查了向量的求模问题,是基础题目.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:解答题
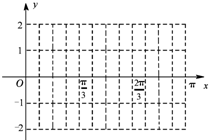 设函数f(x)=2sin(2x+φ)(0<φ<π),y=f(x)图象的一个对称中心是$(\frac{π}{3},0)$.
设函数f(x)=2sin(2x+φ)(0<φ<π),y=f(x)图象的一个对称中心是$(\frac{π}{3},0)$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 8 | C. | -1 | D. | -8 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 空间四边形ABCD中,若向量$\overrightarrow{AB}$=(-3,5,2),$\overrightarrow{CD}$=(-7,-1,-4)点E,F分别为线段BC,AD的中点,则$\overrightarrow{EF}$的坐标为( )
空间四边形ABCD中,若向量$\overrightarrow{AB}$=(-3,5,2),$\overrightarrow{CD}$=(-7,-1,-4)点E,F分别为线段BC,AD的中点,则$\overrightarrow{EF}$的坐标为( )| A. | (2,3,3) | B. | (-2,-3,-3) | C. | (5,-2,1) | D. | (-5,2,-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com