
分析 证明直线与平面垂直,根据定义,需证明直线与平面内的任一直线垂直,故可利用平面向量基本定理,将平面内的任一向量用一组基底表示,证明当直线与基底垂直时,就垂直于平面内的任一向量,利用数量积运算即可得证.
解答 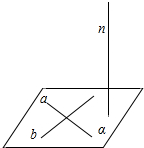 解:设直线a的方向向量为$\overrightarrow{a}$,直线b的方向向量为$\overrightarrow{b}$,直线n的方向向量为$\overrightarrow{n}$,
解:设直线a的方向向量为$\overrightarrow{a}$,直线b的方向向量为$\overrightarrow{b}$,直线n的方向向量为$\overrightarrow{n}$,
∵a,b是平面α内的两条相交直线,
∴$\overrightarrow{a}$与$\overrightarrow{b}$是平面α内的两个不共线向量,设平面α内的任一向量为$\overrightarrow{m}$,由平面向量基本定理,存在唯一实数λ,μ,使:$\overrightarrow{m}$=λ$\overrightarrow{a}$+μ$\overrightarrow{b}$,
又∵n⊥a,n⊥b,
∴$\overrightarrow{n}$•$\overrightarrow{a}$=0,$\overrightarrow{n}$•$\overrightarrow{b}$=0,
∴$\overrightarrow{n}$•$\overrightarrow{m}$=$\overrightarrow{n}$•(λ$\overrightarrow{a}$+μ$\overrightarrow{b}$)=λ$\overrightarrow{n}•\overrightarrow{a}$+μ$\overrightarrow{n}•\overrightarrow{b}$=0
∴$\overrightarrow{n}$⊥$\overrightarrow{m}$,
∴直线n垂直于平面α内的任意直线,由线面垂直的定义得:l⊥α
点评 本题考查了直线与平面垂直的判定定理及其证明方法,平面向量基本定理的应用,利用平面向量解决几何问题的方法,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 10-$\frac{3\sqrt{41}}{2}$ | B. | 10+$\frac{3\sqrt{41}}{2}$ | C. | 10-$\frac{\sqrt{41}}{2}$ | D. | 10+$\frac{\sqrt{41}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
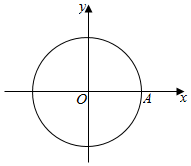 如图,圆周上点A依逆时针方向做匀速圆周运动,已知A点1分钟转过θ(0°<θ<180°),2分钟到第三象限,16分钟后回到原来的位置,求θ.
如图,圆周上点A依逆时针方向做匀速圆周运动,已知A点1分钟转过θ(0°<θ<180°),2分钟到第三象限,16分钟后回到原来的位置,求θ.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (-2$\sqrt{13}$+8,1) | D. | ($\frac{1}{2}$,-2$\sqrt{13}$+8) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com