
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 12 |
| 1 |
| 12 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 8 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| ||
|
| 1 |
| 36 |
| 11 |
| 72 |



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
|
| x-2y-9 |
| y+2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
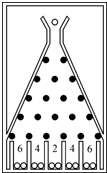 ��һ����б���õľ���ľ���϶���һ�����硰���������Ρ�����������������֮�����п�϶��Ϊͨ�������϶��µ�1��2������֮����1����϶����2��3������֮����2����϶����5��6������֮����5����϶����ͼ����ij�˽�һ��������ӵ�1�еĿ�϶���¹�����������������2�о��е�����������ȵĸ��ʹ����2�е����϶���ҿ�϶���Ժ��������Ʒ�ʽ�������¹����������5�е�ijһ����϶����ľ���·���Ӧ����ۣ����������벻ͬ��۵õ��ķ�������ͼ��ʾ��
��һ����б���õľ���ľ���϶���һ�����硰���������Ρ�����������������֮�����п�϶��Ϊͨ�������϶��µ�1��2������֮����1����϶����2��3������֮����2����϶����5��6������֮����5����϶����ͼ����ij�˽�һ��������ӵ�1�еĿ�϶���¹�����������������2�о��е�����������ȵĸ��ʹ����2�е����϶���ҿ�϶���Ժ��������Ʒ�ʽ�������¹����������5�е�ijһ����϶����ľ���·���Ӧ����ۣ����������벻ͬ��۵õ��ķ�������ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
A��a��[
| ||||
B��a��[0��
| ||||
C��a��[
| ||||
D��(
|
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
| A��{x|x��1} | ||||
B��{x|x��-
| ||||
C��{x|x��
| ||||
D��{x|x��-
|
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com