Question

20．四面体ABCD及其三视图如图1，2所示．

（1）求四面体ABCD的体积；
（2）若点E为棱BC的中点，求异面直线DE和AB所成角的余弦值．

Answer 1

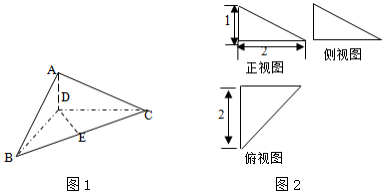
分析 （1）根据直角三角形性质，得：BD⊥DC，AD⊥DC，由此能示出四面体ABCD的体积．
（2）取AC中点F，连DF，EF，则∠DEF为AB与DE所成角或补角．由此能示出异面直线DE和AB所成角的余弦值．

解答 解：（1）根据直角三角形性质，得：BD⊥DC，AD⊥DC，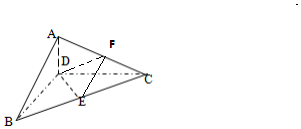
∴l₁=AD=1，${S_{BDC}}=2×2×\frac{1}{2}=2$，
∴四面体ABCD的体积$V=\frac{1}{3}×\frac{1}{2}×2×2×1=\frac{2}{3}$．
（2）取AC中点F，连DF，EF，则∠DEF为AB与DE所成角或补角．
$PE=\frac{1}{2}AB=\frac{{\sqrt{5}}}{2}，DE=\frac{2S}{PC}=\frac{4}{{2\sqrt{2}}}=\sqrt{2}，DP=\frac{1}{2}AC=\frac{{\sqrt{5}}}{2}$，
∴$cosθ=\frac{{\frac{5}{4}+2-\frac{5}{4}}}{{\sqrt{10}}}=\frac{2}{{\sqrt{10}}}=\frac{{\sqrt{10}}}{5}$．
所以异面直线DE和AB所成角的余弦值$\frac{{\sqrt{10}}}{5}$．

点评 本题考查四棱锥的体积的求法，考查异面直线所成角的余弦值的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．