
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 12 |
| 2 |
| 17 |
| 2 |
|


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| 几何证明选讲 | 坐标系与参数方程 | 不等式选讲 | 合计 | |
| 男同学 | 12 | 4 | 6 | 22 |
| 女同学 | 0 | 8 | 12 | 20 |
| 合计 | 12 | 12 | 18 | 42 |
| 几何类 | 代数类 | 总计 | |
| 男同学 | |||
| 女同学 | |||
| 总计 |
查看答案和解析>>
科目:高中数学 来源: 题型:
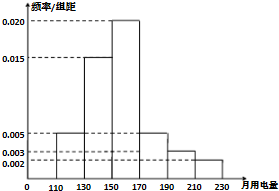 2013年第三季度,国家电网决定对城镇居民用电计费标准作出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图,如图所示.
2013年第三季度,国家电网决定对城镇居民用电计费标准作出调整,并根据用电情况将居民分为三类:第一类的用电区间在(0,170],第二类在(170,260],第三类在(260,+∞)(单位:千瓦时).某小区共有1000户居民,现对他们的用电情况进行调查,得到频率分布直方图,如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:
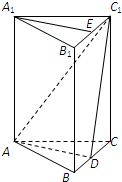 如图,在直三棱柱ABC-A1B1C1中,AB=AC,点D为BC中点,点E在线段B1C1上.
如图,在直三棱柱ABC-A1B1C1中,AB=AC,点D为BC中点,点E在线段B1C1上.查看答案和解析>>
科目:高中数学 来源: 题型:
| 甲 | 81 | 79 | 88 | 93 | 84 |
| 乙 | 92 | 75 | 83 | 90 | 85 |
. |
| x |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com