
| A. | $\frac{1}{11}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{10}{11}$ |
分析 设想有12个位置,双方队员按照淘汰的顺序坐,有${C}_{12}^{6}$种比赛结果,由红队有3名队员波淘汰且最后战胜黄队,知第11个位置和第12个位置是红队队员,第10个位置是黄队队员,由此能求出红队有3名队员波淘汰且最后战胜黄队的概率.
解答 解:设想有12个位置,双方队员按照淘汰的顺序坐,
有${C}_{12}^{6}$种坐法,也就是有${C}_{12}^{6}$种比赛结果,
∵红队有3名队员波淘汰且最后战胜黄队,
∴第11个位置和第12个位置是红队队员,第10个位置是黄队队员,有${C}_{9}^{6}$种坐法,
∴红队有3名队员波淘汰且最后战胜黄队的概率是p=$\frac{{C}_{9}^{6}}{{C}_{12}^{6}}$=$\frac{1}{11}$.
故选:A.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意等价转化思想的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
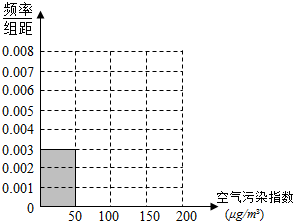 空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.| 空气污染指数(单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | B. | $\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{2}\overrightarrow{AD}$ | C. | $\frac{3}{4}\overrightarrow{AB}$+$\frac{1}{4}\overrightarrow{AD}$ | D. | $\frac{1}{2}\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
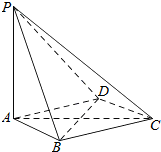 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com