
分析 (1)向量的坐标运算和向量的数量积的坐标运算计算即可,
(2)若$\overrightarrow{c}$与$\overrightarrow{a}$夹角为钝角,则则$\overrightarrow{c}$•$\overrightarrow{a}$<0,问题得以解决.
解答 解:(1)∵$\overrightarrow{a}$=(1,2),$\overrightarrow{b}$=(2,2),
∴2$\overrightarrow{a}$-$\overrightarrow{b}$=(2-2,4-2)=(0,2),2$\overrightarrow{a}$+$\overrightarrow{b}$=(2+2,4+2)=(4,6),
∴(2$\overrightarrow{a}$-$\overrightarrow{b}$)•(2$\overrightarrow{a}$+$\overrightarrow{b}$)=0×4+2×6=12;
(2)若$\overrightarrow{c}$与$\overrightarrow{a}$夹角为钝角,则$\overrightarrow{c}$•$\overrightarrow{a}$<0,
$\overrightarrow{c}$•$\overrightarrow{a}$=(-3,λ)•(1,2)=-3+2λ<0,即 λ<$\frac{3}{2}$,
且$\overrightarrow{c}$与$\overrightarrow{a}$不能方向,即-3×2-λ≠0,解得λ≠-6,
故λ的范围为λ>$\frac{3}{2}$,
点评 本题考查了向量的坐标运算和向量的数量积的坐标运算,以及向量的夹角的问题,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3\sqrt{10}}{10}$ | B. | -$\frac{\sqrt{10}}{10}$ | C. | $\frac{2\sqrt{5}}{5}$ | D. | $\frac{3\sqrt{10}}{10}$或-$\frac{\sqrt{10}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{a}{c}>\frac{b}{d}$ | B. | ac>bd | C. | a2+c2>b2+d2 | D. | a+c>b+d |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 运动时间不超过2小时 | 运动时间超过2小时 | 合计 | |
| 男生 | 10 | 20 | 30 |
| 女生 | 13 | 7 | 20 |
| 合计 | 23 | 27 | 50 |
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
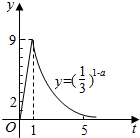 我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线
我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{11}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{10}{11}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1<a≤4 | B. | 1<a≤8 | C. | 1<a≤12 | D. | 1<a≤24 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com