
| A. | 1<a≤4 | B. | 1<a≤8 | C. | 1<a≤12 | D. | 1<a≤24 |
分析 函数f(x)=loga(x3-2ax)(a>0且a≠1)在(4,+∞)上单调递增,根据幂函数类函数的递增趋势知当自变量大到一定程度,内层函数一定是增函数,由此可以判断出外层函数一定是增函数,即底数大于1,又由复合函数的单调性可以判断出内层函数在(4,+∞)上单调递增,故可以导数在该区间上恒正来得到参数的不等式,由此解出参数a的取值范围.
解答 解:函数f(x)=loga(x3-2ax)(a>0且a≠1)在(4,+∞)上单调递增,
故外层函数是增函数,由此得a>1,
又内层函数在区间在(4,+∞)上单调递增,
令t=x3-2ax
则t′=3x2-2a≥0在(4,+∞)上恒成立,
即3x2≥2a在(4,+∞)上恒成立
故2a≤48,即a≤24,
又由真数大于0,故,64-8a≥0,
故a≤8,由上得a的取值范围是1<a≤8,
故选:B.
点评 本题的考点是复合函数的单调性,本题考查依据复合函数的单调性转化出函数中参数所满足的不等式或者方程求参数,这类题是复合函数考查的一大类题型,难度较大,要注意转化的等价性,比如在本题中就容易忘记真数大于为这一隐含条件.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$$\overrightarrow{AB}$+$\frac{1}{2}$$\overrightarrow{AD}$ | B. | $\frac{3}{4}$$\overrightarrow{AB}$+$\frac{1}{2}\overrightarrow{AD}$ | C. | $\frac{3}{4}\overrightarrow{AB}$+$\frac{1}{4}\overrightarrow{AD}$ | D. | $\frac{1}{2}\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AD}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
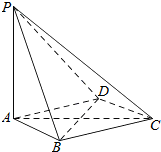 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,1) | B. | (-2,6) | C. | [-2,6] | D. | {-2,6} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com