
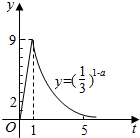 我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线
我国科研人员屠呦呦法相从青篙中提取物青篙素抗疟性超强,几乎达到100%,据监测:服药后每毫升血液中的含药量y(微克)与时间r(小时)之间近似满足如图所示的曲线分析 (1)利用函数的图象,求出函数的解析式即可.
(2)利用分段函数列出不等式,求解即可.
解答 解:(1)由题意,设:f(t)=$\left\{\begin{array}{l}{kt,t∈[0,1]}\\{({\frac{1}{3})}^{t-a},t>1}\end{array}\right.$,当t=1时,由y=9,可得k=9,由$({\frac{1}{3})}^{1-a}=9$,可得a=3,
则f(t)=$\left\{\begin{array}{l}{9t,t∈[0,1]}\\{(\frac{1}{3})^{t-3},t>1}\end{array}\right.$,
(2)由每毫升血液中含药量不少于$\frac{1}{9}$微克时,治疗有效,即y≥$\frac{1}{9}$,得$\left\{\begin{array}{l}{0≤t≤1}\\{9t≥\frac{1}{9}}\end{array}\right.$,或$\left\{\begin{array}{l}{t>1}\\{({\frac{1}{3})}^{t-3}≥\frac{1}{9}}\end{array}\right.$,
解得:$\frac{1}{81}≤t≤5$.
点评 本题考查分段函数的解析式的求法,考查分析问题解决问题的能力.


 阶梯计算系列答案
阶梯计算系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
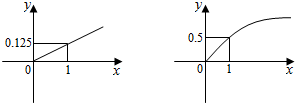 某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).
某家庭进行理财投资,根据长期收益率市场预测,投资债券等稳健型产品的收益与投资额成正比,投资股票等风险型产品的收益与投资额的算术平方根成正比,已知投资1万元时两类产品的收益分别为0.125万元和0.5万元(如图).查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(-1)<f(-3) | B. | f(0)>f(1) | C. | f(-1)<f(1) | D. | f(-3)<f(-5) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
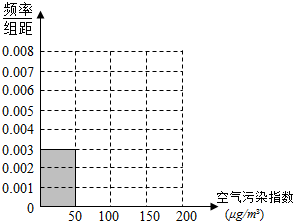 空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.
空气污染,又称为大气污染,是指由于人类活动或自然过程引起某些物质进入大气中,呈现出足够的浓度,达到足够的时间,并因此危害了人体的舒适、健康和福利或环境的现象.全世界也越来越关注环境保护问题.| 空气污染指数(单位:μg/m3) | [0,50] | (50,100] | (100,150] | (150,200] |
| 监测点个数 | 15 | 40 | y | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com