
分析 (1)把75°变为45°+30°,然后利用两角和的正弦函数公式化简后,再利用特殊角的三角函数值即可求出值.
(2)由已知利用余弦定理可求cosC的值,利用特殊角的三角函数值即可得解.
解答 解:(1)sin75°=sin(45°+30°)=sin45°cos30°+cos45°sin30°=$\frac{\sqrt{2}}{2}×\frac{\sqrt{3}}{2}$+$\frac{\sqrt{2}}{2}×\frac{1}{2}$=$\frac{\sqrt{6}+\sqrt{2}}{4}$.
(2)∵a2-c2+b2=ab,
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{ab}{2ab}$=$\frac{1}{2}$,
∵C∈(0,π),
∴C=$\frac{π}{3}$.
点评 本题主要考查了两角和的正弦函数公式,特殊角的三角函数值,余弦定理的综合应用,考查了转化思想,属于基础题.


 小学能力测试卷系列答案
小学能力测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 顶点 | B. | 长轴长 | C. | 离心率 | D. | 焦点 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
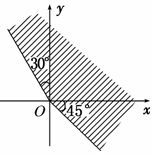
| A. | {α|-45°≤α≤120°} | B. | {α|120°≤α≤315°} | ||
| C. | {α|-45°+k•360°≤α≤120°+k•360°,k∈Z} | D. | {α|120°+k•360°≤α≤315°+k•360°,k∈Z} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45° | B. | 135° | C. | 45°或135° | D. | 以上都不对 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com