
分析 f(x+$\frac{1}{2}$)=$\frac{{x}^{2}+xcosx+2017}{{x}^{2}+2017}$=1+$\frac{xcosx}{{x}^{2}+2017}$,可得$f(\frac{1}{2}-x)$=1-$\frac{xcosx}{{x}^{2}+2017}$,f(x+$\frac{1}{2}$)+$f(\frac{1}{2}-x)$=2,f(1-x)+f(x)=2,再利用“倒序相加”即可得出.
解答 解:∵f(x+$\frac{1}{2}$)=$\frac{{x}^{2}+xcosx+2017}{{x}^{2}+2017}$=1+$\frac{xcosx}{{x}^{2}+2017}$,
∴$f(\frac{1}{2}-x)$=1-$\frac{xcosx}{{x}^{2}+2017}$,
∴f(x+$\frac{1}{2}$)+$f(\frac{1}{2}-x)$=2,
∴f(1-x)+f(x)=2,
则2$\sum_{i=1001}^{1016}$f($\frac{i}{2017}$)=$\sum_{i=1001}^{1016}$f($\frac{i}{2017}$)+$\sum_{i=1001}^{1016}f(\frac{2017-i}{2017})$=2×16=32.
∴$\sum_{i=1001}^{1016}$f($\frac{i}{2017}$)=16.
故答案为:16.
点评 本题考查了“倒序相加”、函数的奇偶性、数列求和,考查了推理能力 与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
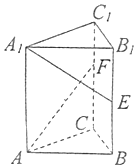 在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )
在三棱柱ABC-A1B1C1中,底面为正三角形,侧棱垂直底面,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,且$BE={B_1}E,{C_1}F=\frac{1}{3}C{C_1}$,则异面直线A1E与AF所成角的余弦值为( )| A. | $-\frac{{\sqrt{2}}}{6}$ | B. | $\frac{{\sqrt{2}}}{6}$ | C. | $-\frac{{\sqrt{2}}}{10}$ | D. | $\frac{{\sqrt{2}}}{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图古铜钱外圆内方,外圆直径为4cm,中间是边长为1cm的正方形孔,随机地在古铜钱所在圆内任取一点,则该点刚好位于孔中的概率是$\frac{1}{4π}$.
如图古铜钱外圆内方,外圆直径为4cm,中间是边长为1cm的正方形孔,随机地在古铜钱所在圆内任取一点,则该点刚好位于孔中的概率是$\frac{1}{4π}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | (¬p)∨(¬q) | C. | (¬p)∧q | D. | p∧(¬q) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com