
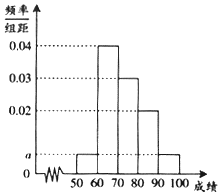
 某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].
某校100位学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60)、[60,70)、[70,80)、[80,90)、[90,100].| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x::y | 1:1 | 2:1 | 3:4 | 4:5 |
分析 解:(1)由频率分布直方图中小矩形的面积和为1,能求出a.
(2)根据频率分布直方图,能估计这100名学生语文成绩的中位数.
(3)由这100名学生的语文成绩某些分数段的人数x与数学成绩相应分数段的人数y之比的表格,能求出数学成绩在[50,90)外的人数.
解答 解:(1)由频率分布直方图中小矩形的面积和为1,
得:0.2+0.3+0.4+20a=1,
解得a=0.005.
(2)区间[50,70)的概率和为0.05+0.4=0.45,
则区间[70,80)中还需拿出概率0.05的区域才到达概率为0.5,
即区间[70,80]要拿出$\frac{1}{6}$的区域,
故中位数为$70+\frac{1}{6}×10=71\frac{2}{3}$.
(3)这100名学生的语文成绩某些分数段的人数x与数学成绩相应分数段的人数y之比如下表所示:
| 分数段 | [50,60) | [60,70) | [70,80) | [80,90) |
| x:y | 1:1 | 2:1 | 3:4 | 4:5 |
| x | 5人 | 40人 | 30人 | 20人 |
| y | 5人 | 20人 | 40人 | 25人 |
点评 本题考查频率分布直方图的应用,考查数据处理能力、读图识图能力,是中档题,解题时要认真审题,注意频率分布直方图的性质的合理运用.


科目:高中数学 来源: 题型:选择题
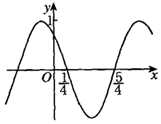 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的部分图象如图所示,则下列说法错误的是( )| A. | ω=π | |
| B. | φ=$\frac{π}{4}$ | |
| C. | f(x)的单调减区间为(2k-$\frac{1}{4}$,2k+$\frac{3}{4}$),k∈Z | |
| D. | f(x)的对称中心是(k+$\frac{1}{4}$,0),k∈Z |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (2,+∞) | C. | (-∞,-6) | D. | (-6,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧(¬q) | D. | (¬p)∧q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com