
����Ŀ���ס��������и�װ�д�С��ͬ��С��9�������м״��к�ɫ����ɫ����ɫС��ĸ����ֱ�Ϊ2��3��4���Ҵ��к�ɫ����ɫ����ɫС��ĸ�����Ϊ3��ij�������ִӼ״���ȡ�������ִ��Ҵ���ȡ��
��1���������ָ�ȡһ������ֻ������ȡ������ɫ��ͬ�ĸ��ʣ�
��2����һ����ͬһ����ȡ���������������ɫ��ͬ������ȡ���óɹ���ij�˵�һ��������ȡ���ڶ���������ȡ��������ȡ��Ļ�óɹ��Ĵ���Ϊ�������X����X�ķֲ��к���ѧ������
���𰸡���1��![]() ����2���ֲ������������
����2���ֲ������������![]() ��
��
��������
���������������Ҫ������ʡ���ɢ����������ķֲ��к���ѧ�����Ȼ���֪ʶ������ѧ���ķ��������������������ת��������������������һ�ʣ���������ȥ�������ָ�ȡһ����ȡ��ɫ��ͬ�����������ȡ��ɫ��Ϊ��ɫ����Ϊ��ɫ����Ϊ��ɫ��������ڶ��ʣ��ȷֱ������������ȡ��������ɫ��ͬ�ĸ��ʣ������ö����¼���������ȡ��Ļ�óɹ��Ĵ���Ϊ0�Ρ�1�Ρ�2�εĸ��ʣ��г��ֲ��У�����![]() ������ѧ������
������ѧ������
�����������1�����¼�![]() Ϊ��������ȡ����ͬɫ���� ��
Ϊ��������ȡ����ͬɫ���� ��![]()
�����⣬![]() �Ŀ���ȡֵΪ0��1��2��
�Ŀ���ȡֵΪ0��1��2��
������ȡ��������ɫ��ͬ�ĸ���Ϊ![]()
������ȡ��������ɫ��ͬ�ĸ���Ϊ![]()
![]()
![]()
![]()
���ԣصķֲ���Ϊ��
�� | 0 | 1 | 2 |
�� |
|
|
|
![]()


 ��ʦ�㾦�ִʾ��ƪϵ�д�
��ʦ�㾦�ִʾ��ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��Ϊ�Ǹ�����������
��Ϊ�Ǹ�����������![]() �ļӷ�ʱ��λ������λ�����磬
�ļӷ�ʱ��λ������λ�����磬![]() �������
�������![]() Ϊ���ġ�����ԣ���
Ϊ���ġ�����ԣ���![]() ��Ϊ��������
��Ϊ��������![]() ��ֵ����ôֵΪ2964�ġ��ġ�����Եĸ����ǣ� ��
��ֵ����ôֵΪ2964�ġ��ġ�����Եĸ����ǣ� ��
A. 525 B. 1050 C. 432 D. 864
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڼ�����ϵ�У��� P�ļ������� ![]() ������ C�ļ����귽��Ϊ
������ C�ļ����귽��Ϊ ![]() ���Լ���Ϊ����ԭ�㣬����Ϊ x��������Ὠ��ƽ��ֱ������ϵ��б��Ϊ��1��ֱ�� l������P��
���Լ���Ϊ����ԭ�㣬����Ϊ x��������Ὠ��ƽ��ֱ������ϵ��б��Ϊ��1��ֱ�� l������P��
��1��д��ֱ�� l�IJ������̺����� C��ֱ�����귽�̣�
��2����ֱ�� l������C�ཻ������A��B���� ![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ����С������Ϊ
����С������Ϊ![]() ����ֱ��
����ֱ��![]() ����ͼ���һ���Գ��ᣮ
����ͼ���һ���Գ��ᣮ
��1������![]() �Ľ���ʽ��
�Ľ���ʽ��
��2����![]() ����
����![]() ��
��![]() ��
��![]() ���Եı߷ֱ�Ϊ
���Եı߷ֱ�Ϊ![]() ��
��![]() ��
��![]() ����
����![]() ��
��![]() ����
����![]() ������
������![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��������![]() ��ͼ������ƽ��
��ͼ������ƽ��![]() ����λ���ٽ����õ�ͼ����ÿһ��������겻�䣬�������쳤Ϊԭ����
����λ���ٽ����õ�ͼ����ÿһ��������겻�䣬�������쳤Ϊԭ����![]() �������õ���ͼ���Ӧ�ĺ�������
�������õ���ͼ���Ӧ�ĺ�������![]() ����֪����
����֪����![]() ��
��![]() ���Һ���
���Һ���![]() ��
��![]() ��ǡ��
��ǡ��![]() ����㣬����
����㣬����![]() ��
��![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����֪����![]()
����������y=f��x���ڵ�P��2��f��2�����������ߵ�б��Ϊ��6����ʵ��a��
������a=1����f��x���ļ�ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������A��{x|2��x��3}��B��{x|��x+2����x��a����0}������a��1������A��B������____������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�н�������Ϊ�˽�ȫ�и���ѧ�������߷���������ӱ���ȫ�����ѧ���������ȡ��100�˵��������ݽ���ͳ�Ʒ����������ݴ����õ�������ͼ1��ʾ��Ƶ�·ֲ�ֱ��ͼ����������100��ѧ���У����߲�����1.69��ѧ��ֻ��16���������߾�Ҷͼ����ͼ2��ʾ��������������Ƶ�ʹ��Ƹ��и�һѧ�������߸��ʣ�
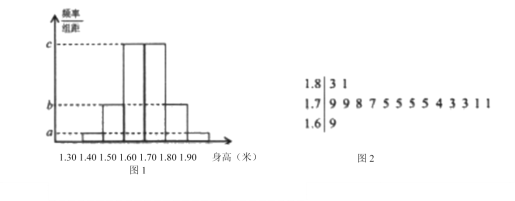
��1������и���ѧ�����߸���1.70�ĸ��ʣ�����ͼ1��![]() ��
��![]() ��
��![]() ��ֵ��
��ֵ��
��2�����Ӹ��и���ѧ�������ѡȡ3��ѧ������![]() Ϊ������
Ϊ������![]() ��ѧ����������
��ѧ����������![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
��3��������![]() ����
����![]() ��
��![]() ����Ʊ���
����Ʊ���![]() �����������̬�ֲ�
�����������̬�ֲ�![]() �ĸ��ʷֲ���������и���ѧ�������������������̬�ֲ�
�ĸ��ʷֲ���������и���ѧ�������������������̬�ֲ�![]() �ĸ��ʷֲ�������Ϊ���и���ѧ�������߷��������������ģ����жϸ��и���ѧ�������߷��������Ƿ���������˵�����ɣ�
�ĸ��ʷֲ�������Ϊ���и���ѧ�������߷��������������ģ����жϸ��и���ѧ�������߷��������Ƿ���������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() ������һ������
������һ������![]() ��ʹ�ò���ʽ
��ʹ�ò���ʽ![]() ����������
����������![]() ��
��![]() �����.
�����.
��1���Ը����������![]() ��ֵ��
��ֵ��
��2���ڣ�1�����ý��۵�������֤������![]() ��
��
��3�������������⣬ijͬѧ��ȷ�ز���������![]() ��������һ������
��������һ������![]() ��ʹ�ò���ʽ
��ʹ�ò���ʽ![]() ����������
����������![]() ��
��![]() ��
��![]() ����������۲�����
����������۲�����![]() ������
������![]() �Ĺ��ɣ������������
�Ĺ��ɣ������������![]() ��
��![]() ��
��![]() ��
��![]() ��ص����⣮
��ص����⣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f��x��=xlnx��ax��g��x��=��x2��2��
��1����һ��x�ʣ�0��+�ޣ���f��x����g��x�����������ʵ��a��ȡֵ��Χ��
��2����a=��1ʱ������f��x��������[m��m+3]��m��0���ϵ���ֵ��
��3��֤������һ��x�ʣ�0��+�ޣ������� ![]() ������
������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com