Question

3．如图，AB是圆O的直径，PA直圆O所在的平面，C是圆O上的点．
（1）求证：平面PAC⊥平面PBC．
（2）设Q为PA的中点，G为△AOC的重心，求证：QG∥平面PBC．

Answer 1

分析 （1）要证明平面PAC垂直于平面PBC，需证明平面PBC内的直线BC，垂直平面PAC内的两条相交直线PA、AC即可．
（2）连接OG并延长交AC于点M，则由重心的性质可得M为AC的中点．利用三角形的中位线性质，证明OM∥BC，QM∥PC，可得平面OQM∥平面PBC，从而证明QG∥平面PBC．

解答 证明：（1）由AB是圆的直径，得AC⊥BC；
由PA垂直于圆O所在的平面，得PA⊥平面ABC；又BC?平面ABC，得PA⊥BC．
又PA∩AC=A，PA?平面PAC，AC?平面PAC，
所以BC⊥平面PAC，又BC?平面PBC，所以平面PAC⊥平面PBC．
（2）连接OG并延长交AC于M，
连接QM，QO．由G为△AOC的重心，知M为AC的中点，
由Q为PA的中点，则QM∥PC，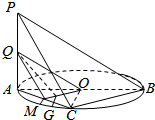
又O为AB中点，得OM∥BC．
因为QM∩MO=M，QM?平面QMO，
MO?平面QMO，BC∩PC=C，BC?平面PBC，PC?平面PBC，
所以平面QMO∥平面PBC．
因为QG?平面QMO，所以QG∥平面PBC．

点评 本题考查直线与平面平行与垂直的判定，考查空间想象能力，逻辑思维能力，考查了转化思想，属于基本知识的考查．