
分析 (1)由题意可知:设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),半焦距为c,由题意可知:e=$\frac{c}{a}$=$\frac{1}{2}$,即a=2c,a+c=3,b2=a2-c2,即可求得a和b的值,即可求得椭圆的标准方程;
(2)设直线l的方程为y=kx+m,代入椭圆方程,由△>0 求得3+4k2>m2,由韦达定理求得x1+x2=-$\frac{8km}{3+4{k}^{2}}$,x1•x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$,由以AB为直径的圆过原点,$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,由向量数量积的坐标表示x1•x2+y1•y2=0,求得7m2=12+12k2,代入即可求得m2>$\frac{3}{4}$,7m2=12+12k2≥12,即可求得截距y轴上截距的取值范围.
解答 解:(1)由椭圆的焦点在x轴上,则设椭圆C的方程为$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),半焦距为c.
由椭圆的离心率e=$\frac{c}{a}$=$\frac{1}{2}$,即a=2c,
由椭圆C上的点到右焦点的最大距离3,
∴a+c=3,解得:a=2,c=1,
由b2=a2-c2=3,
∴椭圆C的标准方程:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(2)设直线l的方程为y=kx+m,
由$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,整理得:(3+4k2)x2+8kmx+4m2-12=0,
△=(8km)2-4(3+4k2)(4m2-12)>0,整理得:3+4k2>m2,
设A(x1,y1),B(x2,y2),则x1+x2=-$\frac{8km}{3+4{k}^{2}}$,x1•x2=$\frac{4{m}^{2}-12}{3+4{k}^{2}}$,
y1•y2=(kx1+m)(kx2+m)=k2x1•x2+km(x1+x2)+m2,
以AB为直径的圆过原点,
∴OA⊥OB,则$\overrightarrow{OA}$•$\overrightarrow{OB}$=0,
∴x1•x2+y1•y2=0,即x1•x2+k2x1•x2+km(x1+x2)+m2=0,
则(1+k2)x1•x2+km(x1+x2)+m2=0,
(1+k2)•$\frac{4{m}^{2}-12}{3+4{k}^{2}}$-km•$\frac{8km}{3+4{k}^{2}}$+m2=0,化简得:7m2=12+12k2,
将k2=$\frac{7}{12}$m2-1,代入3+4k2>m2,3+4($\frac{7}{12}$m2-1)>m2,
解得:m2>$\frac{3}{4}$,
又由7m2=12+12k2≥12,
从而m2≥$\frac{12}{7}$,m≥$\frac{2\sqrt{21}}{7}$或m≤-$\frac{2\sqrt{21}}{7}$.
∴实m的取值范围(-∞,-$\frac{2\sqrt{21}}{7}$]∪[$\frac{2\sqrt{21}}{7}$,+∞).
点评 本题考查椭圆的标准方程,考查直线与椭圆的位置关系,考查韦达定理及向量数量积的坐标表示,考查计算能力,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
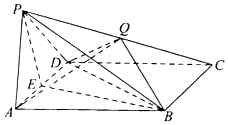 已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.
已知四棱锥P-ABCD中,底面ABCD是菱形,PA=PD,∠BAD=60°,E是AD的中点,点Q在侧棱PC上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 4 | C. | 5 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com