
| A. | y=±$\sqrt{3}$x | B. | y=±2x | C. | y=±$\sqrt{2}$x | D. | y=±$\sqrt{5}$x |
分析 求得双曲线的左顶点A(-a,0),F1(-c,0),由平面几何知识可得|AP|=|AF1|,求得P的坐标,运用两点的距离公式,结合a,b,c的关系,化简整理可得c=2a,b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$a,即可得到所求双曲线的方程.
解答 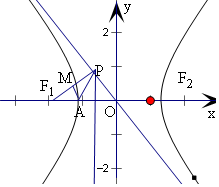 解:双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左顶点A(-a,0),F1(-c,0),
解:双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左顶点A(-a,0),F1(-c,0),
M为线段F1P的中点,且F1P⊥AM,可得|AP|=|AF1|,
OP为渐近线方程:y=-$\frac{b}{a}$x,
P(-$\frac{{a}^{2}}{c}$,yp)即为P(-$\frac{{a}^{2}}{c}$,$\frac{ab}{c}$),
即有$\sqrt{(a-\frac{{a}^{2}}{c})^{2}+(\frac{ab}{c})^{2}}$=c-a,
即有a2(c-a)2+a2b2=c2(c-a)2,
(c2-a2)(c-a)2=a2b2,
可得c-a=a,即c=2a,
b=$\sqrt{{c}^{2}-{a}^{2}}$=$\sqrt{3}$a,
即有双曲线的渐近线方程为y=±$\frac{b}{a}$x,
即为y=±$\sqrt{3}$x.
故选:A.
点评 本题考查双曲线的渐近线方程的求法,注意运用平面几何性质,考查数形结合和化简整理的运算能力,属于中档题.


科目:高中数学 来源:2015-2016学年河南省商丘市高一文下学期期末考数学试卷(解析版) 题型:解答题
已知△ABC的角A、B、C所对的边分别是a、b、c,设向量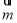 =(a,b),
=(a,b),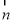 =(sin B,sin A),
=(sin B,sin A),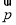 =(b-2,a-2).
=(b-2,a-2).
(Ⅰ)若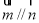 ,判断△ABC的形状;
,判断△ABC的形状;
(Ⅱ)若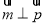 ,边长c=2,角C=
,边长c=2,角C=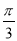 ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2015-2016学年河北省保定市高一上学期期中考试数学试卷(解析版) 题型:解答题
已知y=f(x)是定义在R上的奇函数,且x<0时,f(x)=1+2x.
(1)求函数f(x)的解析式.
(2)画出函数f(x)的图象.
(3)写出函数f(x)单调区间及值域.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\frac{5}{2}$ | C. | $\frac{10}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{AD}$•($\overrightarrow{AB}$-$\overrightarrow{AC}$)=0 | B. | |$\overrightarrow{AB}$+$\overrightarrow{AC}$|≥2|$\overrightarrow{AD}$| | C. | $\overrightarrow{AC}$•$\overrightarrow{AD}$=|$\overrightarrow{AC}$|2 | D. | $\overrightarrow{AC}$•$\frac{\overrightarrow{AD}}{|\overrightarrow{AD|}}$=|$\overrightarrow{AB}$|sinB |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com