
分析 (Ⅰ)由每家煤矿必须整改的概率是1-0.5,且每家煤矿是否整改是相互独立的.代入n次独立重复试验中恰好发生k次的概率公式,即可得到答案;
(Ⅱ)要至少关闭一家煤矿的概率.则表示该煤矿第一次安检不合格,整改后经复查仍不合格,代入分步事件概率乘法公式即可得到结论;
(Ⅲ)由题意,必须整改的煤矿数ξ服从二项分布B(5,0.5),我们计算出ξ的数学期望,根据数学期望易得到平均有多少家煤矿必须整改.
解答 解:(Ⅰ)每家造纸厂必须整改的概率是1-0.5,
且每家造纸厂是否整改是相互独立的.
所以恰好有两家造纸厂必须整改的概率是
P1=${C}_{5}^{2}$×(1-0.5)2×0.53=$\frac{5}{16}$=0.31.
(Ⅱ)某造纸厂被关闭,
即该造纸厂第一次安检不合格,
整改后经复查仍不合格,
所以该造纸厂被关闭的概率是
P2=(1-0.5)×(1-0.8)=0.1,
从而该造纸厂不被关闭的概率是0.9.
由题意,每家造纸厂是否被关闭是相互独立的,
所以至少关闭一家造纸厂的概率是:
P3=1-0.95=0.41;
(Ⅲ)由题设,必须整改的造纸厂数ξ服从二项分布B(5,0.5).
从而ξ的数学期望是Eξ=5×0.5=2.5,
即平均有2.50家造纸厂必须整改.
点评 本小题主要考查相互独立事件概率的计算,运用数学知识解决问题的能力,要想计算一个事件的概率,首先我们要分析这个事件是分类的(分几类)还是分步的(分几步),然后再利用加法原理和乘法原理进行求解.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-∞,2) | B. | (2,+∞) | C. | (-∞,1)∪(1,2) | D. | (-∞,1)∪(2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{7}$ | B. | $\frac{2}{7}$ | C. | $\frac{15}{28}$ | D. | $\frac{19}{28}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
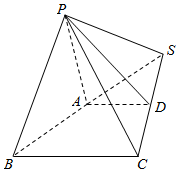 在三棱锥P-SBC中,A,D分别为边SB,SC的中点,且AB=3,BC=8,CD=5.PA⊥BC.
在三棱锥P-SBC中,A,D分别为边SB,SC的中点,且AB=3,BC=8,CD=5.PA⊥BC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
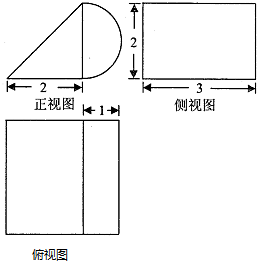
| A. | 4+$\frac{2}{3}π$ | B. | 4+$\frac{3}{2}$π | C. | 6+$\frac{2}{3}π$ | D. | 6+$\frac{3}{2}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 30° | C. | 60° | D. | 120° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com