
已知f(x)=lnx,g(x)=af(x)+f′(x),
(1)求g(x)的单调区间;
(2)当a=1时, ①比较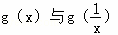 的大小;
的大小;
②是否存在x0>0,使得|g(x)﹣g(x0)|<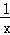 对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由.
对任意x>0成立?若存在,求出x0的取值范围;若不存在,请说明理由.
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案科目:高中数学 来源: 题型:
学校为了解学生课外读物方面的支出情况,抽取了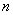 个同学进行调查,结果显示这些同学的支出都在
个同学进行调查,结果显示这些同学的支出都在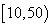 (单位:元),其中支出在
(单位:元),其中支出在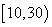 (单位:元)的同学有
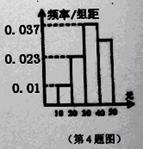
(单位:元)的同学有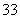 人,其频率分布直方图如下图所示,则支出在
人,其频率分布直方图如下图所示,则支出在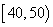 (单位:元)的同学人数是( )
(单位:元)的同学人数是( )
A.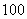 B.
B.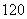 C.
C.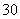 D.
D.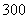
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=ln(ex﹣1)(x>0)( )
|
| A. | 若f(a)+2a=f(b)+3b,则a>b | B. | 若f(a)+2a=f(b)+3b,则a<b |
|
| C. | 若f(a)﹣2a=f(b)﹣3b,则a>b | D. | 若f(a)﹣2a=f(b)﹣3b,则a<b |
查看答案和解析>>
科目:高中数学 来源: 题型:
袋中装有黑球和白球共7个,从中任取2个球都是黑球的概率为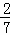 ,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取…,取球后不放回,直到两人中有一人取到白球时终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
,现有甲、乙两人从袋中轮流摸取1球,甲先取,乙后取,然后甲再取…,取球后不放回,直到两人中有一人取到白球时终止,每个球在每一次被取出的机会是等可能的,用ξ表示取球终止所需要的取球次数.
(Ⅰ)求随机变量ξ的分布列及数学期望;
(Ⅱ)求乙取到白球的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
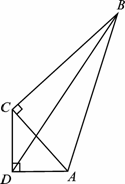
如图,将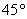 的直角三角板ADC和
的直角三角板ADC和 的直角三角板ABC拼在一起组成平面四边形ABCD,其中
的直角三角板ABC拼在一起组成平面四边形ABCD,其中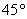 的直角三角板的斜边AC与
的直角三角板的斜边AC与 的直角三角板的
的直角三角板的 所对的直角边重合,若
所对的直角边重合,若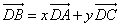 ,则x,y分别等于( )
,则x,y分别等于( )
A.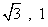 B.
B.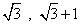 C.
C.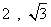 D.
D.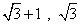
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com