
分析 (1)求得F(-1,0),圆F的半径,运用垂直平分线的性质和椭圆的定义,即可得到所求轨迹方程;
(2)将直线y=kx+$\sqrt{5}$代入椭圆4x2+5y2=20,设G(x1,y1),H(x2,y2),运用韦达定理和判别式,假设($\overrightarrow{OG}$+$\overrightarrow{OH}$)⊥$\overrightarrow{BD}$,运用向量垂直的条件:数量积为0,解方程可得k,即可判断.
解答 解:(1)由题意可得F(-1,0),圆F的半径为2$\sqrt{5}$,
|MF|+|MA|=|MF|+|MP|=|FP|=2$\sqrt{5}$>|FA|=2,
由椭圆的定义可得,M的轨迹为以F,A为焦点,长轴长为2$\sqrt{5}$的椭圆,
即有a=$\sqrt{5}$,c=1,b=$\sqrt{{a}^{2}-{c}^{2}}$=2,
则曲线C的方程为$\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1;
(2)将直线y=kx+$\sqrt{5}$代入椭圆4x2+5y2=20,可得
(4+5k2)x2+10$\sqrt{5}$kx+5=0,①
设G(x1,y1),H(x2,y2),可得x1+x2=-$\frac{10\sqrt{5}k}{4+5{k}^{2}}$,
$\overrightarrow{OG}$+$\overrightarrow{OH}$=(x1+x2,y1+y2),y1+y2=k(x1+x2)+2$\sqrt{5}$=$\frac{8\sqrt{5}}{4+5{k}^{2}}$,
由B(0,$\sqrt{5}$),D(-4,0),可得$\overrightarrow{BD}$=(-4,-$\sqrt{5}$),
若($\overrightarrow{OG}$+$\overrightarrow{OH}$)⊥$\overrightarrow{BD}$,即有($\overrightarrow{OG}$+$\overrightarrow{OH}$)•$\overrightarrow{BD}$=0,
即有-4(x2+x1)-$\sqrt{5}$(y1+y2)=0,
可得-4•(-$\frac{10\sqrt{5}k}{4+5{k}^{2}}$)-$\frac{40}{4+5{k}^{2}}$=0,
解得k=$\frac{\sqrt{5}}{5}$,
当k=$\frac{\sqrt{5}}{5}$时,方程①的判别式为500k2-20(4+5k2)=0不满足题意.
故不存在这样的常数k,使得($\overrightarrow{OG}$+$\overrightarrow{OH}$)⊥$\overrightarrow{BD}$.
点评 本题考查轨迹方程的求法,注意运用垂直平分线的性质和椭圆的定义,考查直线方程和椭圆方程联立,运用韦达定理,同时考查向量垂直的条件:数量积为0,化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-6,2] | B. | [-6,-2] | C. | [-2,6] | D. | $[{2-\sqrt{7}{,_{\;}}2+\sqrt{7}}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
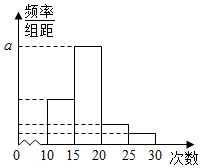 对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
对某校高一年级学生参加社区服务次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:| 分组 | 频数 | 频率 |
| [10,15) | 10 | 0.25 |
| [15,20) | 25 | n |
| [20,25) | m | p |
| [25,30) | 2 | 0.05 |
| 合计 | M | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com