【题目】已知函数
.
（1）若曲线
在点
处的切线与直线
平行，求
的值；
（2）若
，求函数
在区间
上的最小值.
【答案】（1）1（2）见解析
【解析】试题分析：（1）本问主要考查导数几何意义，由于曲线
在点
处的切线与直线
平行，根据两直线平行斜率相等得
，对函数
求导，带入
，即可求出
的值；（2）本问考查利用导数研究函数最值， 
，显然
时， 
，然后对
进行讨论，分别讨论
， 
时
在区间
上的单调性，进而可以求出最小值.这里重点考查分类讨论思想方法在解题中的应用.
试题解析： 
.
（1）由题意可得
，解得
，此时
，
在点
处的切线为
，与直线
平行.
故所求的
值为
．
（2）
，可得
.
①
时， 
在
上恒成立，所以
在
上递增，
所以
在
上的最小值为
.
②当
时， 
， 
随
的变化情况如下：
|
|
|
|
| - |
| + |
| ↓ | 极小 | ↑ |
由上表可知
在
的最小值为
.
综上可知：
当
时， 
在
上的最小值为
；
当
时， 
在
上的最小值为
．
科目：高中数学 来源： 题型：
【题目】已知函数f(x)＝|2x－1|＋|x－2a|.
(1)当a＝1时，求f(x)≤3的解集；
(2)当x∈[1，2]时，f(x)≤3恒成立，求实数a的取值范围．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知a是实数，函数f(x)＝
(x－a)．
(1)求函数f(x)的单调区间；
(2)设g(a)为f(x)在区间[0,2]上的最小值．
①写出g(a)的表达式；
②求a的取值范围，使得－6≤g(a)≤－2.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】以下是解决数学问题的思维过程的流程图：
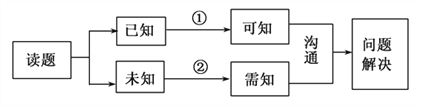
在此流程图中，①、②两条流程线与“推理与证明”中的思维方法匹配正确的是( )
A. 
①—分析法，②—反证法 B. ①—分析法，②—综合法
C. ①—综合法，②—反证法 D. ①—综合法，②—分析法
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】如图，已知圆
：
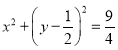经过椭圆
：
（
）的左右焦点
，
，与椭圆
在第一象限的交点为
，且
，
，
三点共线．
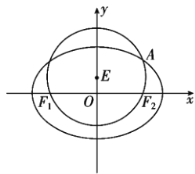
（Ⅰ）求椭圆
的方程；
（Ⅱ）设与直线
（
为原点）平行的直线
交椭圆
于
，
两点．当
的面积取到最大值时，求直线
的方程．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】一个盒子中装有2个红球，4个白球，除颜色外，它们的形状、大小、质量等完全相同
（1）采用不放回抽样，先后取两次，每次随机取一个球，求恰好取到1个红球，七个白球的概率；
（2）采用放回抽样，每次随机抽取一球，连续取3次，求至少有1次取到红球的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
图象上点
处的切线方程与直线
平行（其中
），
.
（Ⅰ）求函数
的解析式；
（Ⅱ）求函数
在
（
）上的最小值；
（Ⅲ）对一切
， 
恒成立，求实数
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
