
【题目】判断下列函数的奇偶性:
(1)![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
(4)![]() ;
;
(5)![]() ;
;
(6)![]() ;
;
(7)![]() ;
;
(8)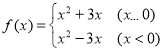
【答案】(1)非奇非偶;(2)既奇又偶;(3)非奇非偶;(4)非奇非偶;(5)偶;(6)奇;(7)奇;(8)偶
【解析】
先求函数的定义域,若定义域不关于原点对称,则该函数是非奇非偶函数;若定义域关于原点对称,且![]() ,则该函数是既奇又偶函数;若定义域关于原点对称,再计算
,则该函数是既奇又偶函数;若定义域关于原点对称,再计算![]() ,看
,看![]() 与
与![]() 、
、![]() 是否相等,然后按照奇偶函数定义判断;确定函数的定义域,有时能化简函数的解析式,以便简化解题过程,如(4)和(7)题;分段函数要分段分别判断;根据以上逐一判断即可.
是否相等,然后按照奇偶函数定义判断;确定函数的定义域,有时能化简函数的解析式,以便简化解题过程,如(4)和(7)题;分段函数要分段分别判断;根据以上逐一判断即可.
解:(1)![]() ,其定义域不关于原点对称,所以该函数是非奇非偶函数;
,其定义域不关于原点对称,所以该函数是非奇非偶函数;
(2)根据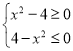 ,所以
,所以![]() 关于原点对称,又
关于原点对称,又![]()
![]() 是既奇又偶函数;
是既奇又偶函数;
(3)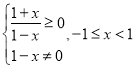 ,其定义域
,其定义域![]() 不关于原点对称,
不关于原点对称,
所以该函数是非奇非偶函数;
(4)![]() 的定义域是
的定义域是![]() 不关于原点对称,
不关于原点对称,
所以该函数是非奇非偶函数;
(5)![]() 的定义域是
的定义域是![]() 关于原点对称,
关于原点对称,
![]() ,所以该函数是偶函数;
,所以该函数是偶函数;
(6)![]() 的定义域是
的定义域是![]() 关于原点对称
关于原点对称
![]() ,所以该函数是奇函数;
,所以该函数是奇函数;
(7)![]() 定义域关于原点对称,此时
定义域关于原点对称,此时![]() ,
,
![]() ,所以该函数是奇函数;
,所以该函数是奇函数;
(8)函数定义域是![]() 关于原点对称,
关于原点对称,
当![]() ,则
,则![]() ,
,![]()
当![]() ,则
,则![]() ,
,![]()
![]() ,
,
所以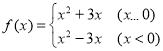 是偶函数
是偶函数


科目:高中数学 来源: 题型:
【题目】为选拔选手参加“中国诗词大会”,某中学举行一次“诗词大赛”活动.为了了解本次竞赛学生的成绩情况,从中抽取了部分学生的分数(得分取正整数,满分为100分)作为样本(样本容量为![]() )进行统计.按照
)进行统计.按照![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在
的分组作出频率分布直方图,并作出样本分数的茎叶图(图中仅列出了得分在![]() ,
, ![]() 的数据).
的数据).
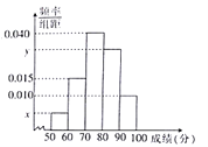
(1)求样本容量![]() 和频率分布直方图中
和频率分布直方图中![]() 、
、![]() 的值;
的值;
(2)在选取的样本中,从竞赛成绩在80分以上(含80分)的学生中随机抽取2名学生参加“中国谜语大会”,设随机变量![]() 表示所抽取的2名学生中得分在
表示所抽取的2名学生中得分在![]() 内的学生人数,求随机变量
内的学生人数,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某次考试结束,甲、乙、丙三位同学聚在一起聊天.甲说:“你们的成绩都没有我高![]() ”乙说:“我的成绩一定比丙高
”乙说:“我的成绩一定比丙高![]() ”丙说:“你们的成绩都比我高
”丙说:“你们的成绩都比我高![]() ”成绩公布后,三人成绩互不相同且三人中恰有一人说得不对,若将三人成绩从高到低排序,则甲排在第______名
”成绩公布后,三人成绩互不相同且三人中恰有一人说得不对,若将三人成绩从高到低排序,则甲排在第______名![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某少数民族的刺绣有着悠久的历史,如图4①,②,③,④为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含f(n)个小正方形.
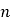
(1)求出f(5)的值;
(2)利用合情推理的“归纳推理思想”,归纳出f(n+1)与f(n)之间的关系式,并根据你得到的关系式求出f(n)的表达式;
(3)求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知点A,B的坐标分别为(3,0),(-3,0),直线AP,BP相交于点P,且它们的斜率之积是-2,求动点P的轨迹方程.
(2)设P(x,y),直线l1:x+![]() y=0,l2:x-
y=0,l2:x-![]() y=0.若点P到l1的距离与点P到l2的距离之积为2,求动点P的轨迹方程.
y=0.若点P到l1的距离与点P到l2的距离之积为2,求动点P的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家收购某种农产品的价格为120元/t,其中征税标准为每100元征收8元(称税率为8个百分点),计划可收购a万t,为减轻农民负担,决定降低税率x个百分点,预计收购量可增加2x个百分点.
(1)写出降低税率后,税收y(万元)与x的关系式;
(2)要使此项税收在税率调整后不低于原计划的78%,试确定x的范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,圆锥PO中,AB是圆O的直径,且AB=4,C是底面圆O上一点,且AC=2![]() ,点D为半径OB的中点,连接PD.
,点D为半径OB的中点,连接PD.
(1)求证:PC在平面APB内的射影是PD;
(2)若PA=4,求底面圆心O到平面PBC的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知从1开始的连续奇数蛇形排列形成宝塔形数表,第一行为1,第二行为3,5,第三行为7,9,11,第四行为13,15,17,19,…,如图所示,在宝塔形数表中位于第![]() 行、第
行、第![]() 列的数记为
列的数记为![]() ,比如
,比如![]() ,
,![]() ,
,![]() .若
.若![]() ,则
,则![]() ______.
______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
以平面直角坐标系的原点![]() 为极点,
为极点, ![]() 轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线
轴的正半轴为极轴,且两个坐标系取相等的长度单位.已知直线![]() 的参数方程为
的参数方程为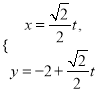 (
(![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为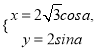 (
(![]() 为参数),曲线
为参数),曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求曲线![]() 和
和![]() 的公共点的极坐标;
的公共点的极坐标;
(2)若![]() 为曲线
为曲线![]() 上的一个动点,求
上的一个动点,求![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com