
分析 (1)运用导数的积的运算法则,和指数和对数的导数公式即可得到所求;
(2)运用导数的商的运算法则,以及正弦和余弦函数的导数,计算即可得到所求.
解答 解:(1)y=exlnx的导数为y′=exlnx+ex•$\frac{1}{x}$=ex(lnx+$\frac{1}{x}$);
(2))y=$\frac{1+cosx}{sinx}$的导数为y′=$\frac{-sinx•sinx-(1+cosx)cosx}{si{n}^{2}x}$
=$\frac{-si{n}^{2}x-cosx-co{s}^{2}x}{si{n}^{2}x}$=$\frac{-1-cosx}{si{n}^{2}x}$.
点评 本题考查导数的运算法则和公式,考查运算能力,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
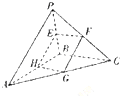 三棱锥P-ABC中,PA=2,BC=3,PA⊥BC,如图所示,作与PA、BC都平行的截面,分别交棱PB、BC、AC、AB于点E、F、G、H,则截面EFGH的最大面积为( )
三棱锥P-ABC中,PA=2,BC=3,PA⊥BC,如图所示,作与PA、BC都平行的截面,分别交棱PB、BC、AC、AB于点E、F、G、H,则截面EFGH的最大面积为( )| A. | 3 | B. | 6 | C. | $\frac{3}{2}$ | D. | $\frac{5}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | -1 | C. | 5 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -3 | B. | 3 | C. | -3i | D. | 3i |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com