
分析 (Ⅰ)由题意知,设点P的坐标为(x,y),则Q的坐标为$({-\frac{1}{2},y})$,求得向量QP,QF,FP,FQ的坐标,运用向量的数量积的坐标表示,化简即可得到所求轨迹的方程;
(Ⅱ)设M(a,b)为圆M的圆心,则b2=2a,求得圆的方程,令x=0,解得交点的纵坐标,即可得到所求定值2.
解答  解:(Ⅰ)由题意知,设点P的坐标为(x,y),则Q的坐标为$({-\frac{1}{2},y})$,
解:(Ⅰ)由题意知,设点P的坐标为(x,y),则Q的坐标为$({-\frac{1}{2},y})$,
因此$\overrightarrow{QP}=({x+\frac{1}{2},0}),\overrightarrow{QF}=({1,-y})$,
$\overrightarrow{FP}=({x-\frac{1}{2},y}),\overrightarrow{FQ}=({-1,y})$.
因$\overrightarrow{QP}•\overrightarrow{QF}=\overrightarrow{FP}•\overrightarrow{FQ}$,
得$({x+\frac{1}{2},0})•({1,-y})=({x-\frac{1}{2},y})•({-1,y})$,
即$x+\frac{1}{2}=\frac{1}{2}-x+{y^2}$,
故动点P(x,y)的坐标满足方程y2=2x;
设N(x0,y0)是y2=2x的任一点,
过N作直线l的垂线,垂足为Q,则有$\overrightarrow{FN}•\overrightarrow{FQ}=\overrightarrow{QN}•\overrightarrow{QF}$,
即y2=2x上的任一点都具有所需的性质.
综上,动点P的轨迹方程为y2=2x;
(Ⅱ)证明:设M(a,b)为圆M的圆心,则b2=2a.
由圆M过点A(1,0),
可得圆M上的点(x,y)满足(x-a)2+(y-b)2=(a-1)2+b2.
令x=0,得y2-2by+2a-1=0,
于是可得圆M与y轴的交点为E1(0,y1)和E2(0,y2),
其中${y_{1,2}}=b±\sqrt{{b^2}-2a+1}=b±1$,
故|E1E2|=|y1-y2|=2是一个常数.
点评 本题考查轨迹方程的求法,注意运用向量的数量积的坐标表示,考查圆的弦长为定值的求法,注意点满足抛物线的方程,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 10 m | B. | 10$\sqrt{2}$ m | C. | 10$\sqrt{3}$ m | D. | 10$\sqrt{6}$ m |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 84 | B. | 252 | C. | 761 | D. | 2284 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-4=0 | B. | $y-2=-\frac{2}{x^2}(x-1)$ | C. | $y-2=\frac{1}{x^2}(x-1)$ | D. | x+2y-4=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
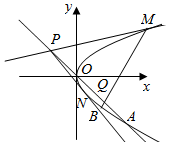 已知抛物线C:y2=2px(p>0)的交点为F,过F且倾斜角为$\frac{π}{4}$的直线l被抛物线C截得的线段长为8.
已知抛物线C:y2=2px(p>0)的交点为F,过F且倾斜角为$\frac{π}{4}$的直线l被抛物线C截得的线段长为8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com