已知函数f(x)=ax2+bx(a,b为常数,且a≠0),x=1时f(x)有最大值,且函数g(x)=f(x)-x只有一个零点.
(1)求函数f(x)的解析式
(2)求实数m,n(m<n),使得f(x)的定义域为[m,n]时,值域是[3m,3n].
解:(1)因为函数f(x)=ax
2+bx(a,b为常数,且a≠0),在x=1时,f(x)有最大值,
所以a<0,对称轴为x=1,即

,所以b=-2a.
g(x)=f(x)-x=ax
2+bx-x=ax
2+(b-1)x,因为函数g(x)=f(x)-x只有一个零点.
所以△=(b-1)
2=0,解得b=1,

.
所以
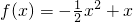
.
(2)由(1)则二次函数的对称轴为x=1,
①当m<n<1时,f (x)在[m,n]上单调递增,f (m)=3m,f (n)=3n,
所以m,n是-

x
2+x=3x的两根.
解得m=-4,n=0;
②当m≤1≤n时,3n=

,解得n=

.不符合题意; …10分
③当1<m<n时,f (x)在[m,n]上单调递减,所以f(m)=3n,f(n)=3m.
即-

m
2+m=3n,-

n
2+n=3m.
相减得-

(m
2-n
2)+(m-n)=3(n-m).
因为m≠n,所以-

(m+n)+1=-3.所以m+n=8.
将n=8-m代入-

m
2+m=3n,
得-m
2+m=3(8-m).但此方程无解.
所以m=-4,n=0时,f (x)的定义域和值域分别是[m,n]和[3m,3n].…
分析:(1)利用函数在x=1时f(x)有最大值,得到抛物线开口向下,且对称轴为x=1,然后利用函数g(x)=f(x)-x只有一个零点,解出a,b.
(2)根据(1)中的解析式,我们分m<n<1,m≤1≤n,1<m<n三种情况分析讨论满足f(x)的定义域为[m,n]时,f(x)的取值范围是[3m,3n]的m,n值,最后综合讨论结果,即可得到答案.
点评:本题考查了二次函数解析式的求法,其中(2)中讨论区间[m,n]与对称轴的关系,是解答二次函数问题最常见的思路.

 ,所以b=-2a.
,所以b=-2a. .
.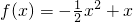 .
. x2+x=3x的两根.
x2+x=3x的两根. ,解得n=
,解得n= .不符合题意; …10分
.不符合题意; …10分 m2+m=3n,-
m2+m=3n,- n2+n=3m.
n2+n=3m. (m2-n2)+(m-n)=3(n-m).
(m2-n2)+(m-n)=3(n-m). (m+n)+1=-3.所以m+n=8.
(m+n)+1=-3.所以m+n=8. m2+m=3n,
m2+m=3n,

 阅读快车系列答案
阅读快车系列答案