练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    1．设计二分法算法，求方程x3-x-1=0在区间[1，1.5]内的解（精度为0.01）．

    分析 函数f（x）=x3-x-1在区间[1，1.5]上连续，从而利用判定定理判断；再利用二分法求值．

    解答 解：函数f（x）=x3-x-1=0在区间[1，1.5]上连续，
    且f（1）=1-1-1＜0，f（1.5）=0.875＞0；
    故函数f（x）=x3-x-1在区间[1，1.5]内内必有零点；
    列表如下，如下：

    f（1）=-1f（1.5）=0.875f（1.25）=-0.2977f（1.375）=0.225
    f（1.3125）=-0.052f（1.34375）=0.083f（1.328125）=0.0148f（1.3203125）＜0
    这个零点的近似值为1.32．

    点评 本题主要考查用二分法求方程的近似解的方法和步骤，体现了转化的数学思想，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    11．ω=-$\frac{1}{2}$+$\frac{\sqrt{3}}{2}$i．则：（1）ω$+\frac{1}{ω}$的值-1；（2）ω2$+\frac{1}{{ω}^{2}}$的值-1．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

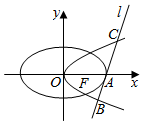    12．如图，抛物线C：y2=8x的焦点为F，椭圆C2：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右顶点为A，离心率为$\frac{1}{2}$，且F为线段OA的中点，O为坐标原点．
    （1）求椭圆C2的标准方程；
    （2）过A点作直线l交C1于B，C两点，求△OBC面积的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．已知函数f（x）=$\frac{1}{2}$x2+alnx（a∈R）
    （1）若函数在点P（1，f（1）处的切线方程与直线x+2y+3=0垂直，求a的值．
    （2）求函数的单调区间；
    （3）记f′（x）为函数f（x）的导函数，若关于x的方程f′（x）-2e=$\frac{lnx}{{x}^{2}}$（e为自然对数的底数）有且仅有两个不同的实根，求a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知cosa=$\frac{4}{5}$，a∈（-$\frac{π}{2}$，0）
    求（1）sin2a，cos2a，tan2a的值
    （2）sin（a+$\frac{π}{3}$），cos（a+$\frac{π}{6}$），tan（a+$\frac{π}{4}$）的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知x2-5ax+25＞0，对x∈R恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．求下列函数的单调区间：y=cos（$\frac{1}{2}$x+$\frac{π}{3}$），x∈[-2π，2π]．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．已知点P（a，4）在抛物线C：x2=2py（p＞0）上，P点到抛物线C的焦点F的距离为5
    （1）求抛物线C的方程；
    （2）已知圆E：x2+y2=2y，过圆心E作直线l与圆E和抛物线C自左而右依次交于A、B、C、D，如果|AB|+|CD|=2|BC|，求直线l的方程：
    （3）过点Q（2，4）的任一直线（不过P点）与抛物线C交于A、B两点，直线AB与直线y=x-4交于点M，记直线PA、PB、PM的斜率分别为k1、k2、k3．问是否存在实数λ，使得$\frac{1}{{k}_{1}}$+$\frac{1}{{k}_{2}}$=$\frac{λ}{{k}_{3}}$，若存在，求出λ的值，若不存在，说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．当-$\frac{π}{2}$≤x≤$\frac{π}{2}$时，函数f（x）=2sin（x+$\frac{π}{3}$）有（　　）
    A．最大值1，最小值-1B．最大值1，最小值-$\frac{1}{2}$
    C．最大值2，最小值-2D．最大值2，最小值-1

    查看答案和解析>>

    同步练习册答案