练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    7．从4种不同的颜色中选择若干种给如图所示的4个方格涂色，每个方格中只涂一种颜色且相邻两格不能涂同一种颜色，则不同的涂色方法共有（　　）
    A．24种B．72种C．96种D．108种

    分析 分类讨论，利用排列知识，即可得出结论．

    解答 解：用两种颜色时，涂法有2${C}_{4}^{2}$种；用三种颜色时，涂法有3${C}_{4}^{3}$${C}_{3}^{1}$${C}_{2}^{1}$种；用四种颜色时，涂法有${A}_{4}^{4}$种，
    所以不同的涂色方法共有12+72+24=108种，
    另解：4×3×3×3=108种．
    故选：D．

    点评 本题考查排列知识，考查分类讨论的数学思想，比较基础．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

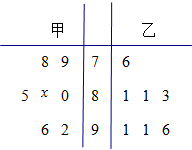    1．某中学高三年级从甲、乙两个班级各选出7名学生参加数学竞赛，他们取得的成绩（满分100分）的茎叶图如图，其中甲班学生的平均分是85．
    （Ⅰ） 计算甲班7位学生成绩的方差s2； 
    （Ⅱ）从成绩在90分以上的学生中随机抽取两名学生，求甲班至少有一名学生的概率．
    参考公式：
    方差${s^2}=\frac{1}{n}[{{{（{{x_1}-\overline x}）}^2}+{{（{{x_2}-\overline x}）}^2}+…+{{（{{x_n}-\overline x}）}^2}}]$，其中$\overline x=\frac{{{x_1}+{x_2}+…+{x_n}}}{n}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知平面α，β和直线a，b，若α∩β=l，a?α，b?β，且平面与平面β不垂直，直线a与直线l不垂直，直线b与直线l不垂直，则（　　）
    A．直线a与直线b可能垂直，但不可能平行
    B．直线a与直线b可能垂直，也可能平行
    C．直线a与直线b不可能垂直，但可能平行
    D．直线a与直线b不可能垂直，也不可能平行

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    15．已知α是第二象限的角，且$sinα=\frac{3}{5}$，则tan2α的值是-$\frac{24}{7}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．为了得到函数y=tan（2x-$\frac{π}{6}$）的图象，可以将函数y=tan2x的图象（　　）
    A．向右平移$\frac{π}{6}$个单位长度B．向右平移$\frac{π}{12}$个单位长度
    C．向左平移$\frac{π}{6}$个单位长度D．向左平移$\frac{π}{12}$个单位长度

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    12．如图所示的算法流程图运行后，输出结果是（　　） 
    A．7B．8C．9D．11

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．某船在海平面A处测得灯塔B在北偏东30°方向，与A相距6.0海里．船由A向正北方向航行8.1海里达到C处，这时灯塔B与船相距多少海里（精确到0.1海里）？B在船的什么方向（精确到1°）？

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．若平面α的一个法向量$\overrightarrow n$=（2，1，1），直线l的一个方向向量为$\overrightarrow a$=（1，2，3），则l与α所成角的正弦值为（　　）
    A．$\frac{\sqrt{17}}{6}$B．$\frac{\sqrt{21}}{6}$C．-$\frac{\sqrt{21}}{6}$D．$\frac{\sqrt{21}}{3}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

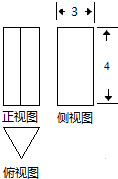    17．如图，一个几何体的三视图，侧视图和正视图均为矩形，俯视图为正三角形，尺寸如图，则该几何体的体积为（　　）
    A．18B．9$\sqrt{3}$C．12$\sqrt{3}$D．4$\sqrt{3}$

    查看答案和解析>>

    同步练习册答案