
分析 (1)通过a=-$\frac{1}{4}$,求出函数的导数,利用导数为0,然后求出极值点,然后求函数f(x)的极值;
(2)利用函数f(x)在区间[2,4]上是减函数,导数小于0恒成立,然后求实数a的取值范围;
(3)问题等价于a(x-1)2+lnx-x+1≤0恒成立,设g(x)=a(x-1)2+lnx-x+1(x≥1),只需g(x)max≤0即可,根据函数的单调性求出g(x)的最大值,从而求出a的范围.
解答 解:(1)当a=-$\frac{1}{4}$时,f′(x)=-$\frac{(x-2)(x+1)}{2x}$(x>0),
则当0<x<2时f'(x)>0,故函数f(x)在(0,2)上为增函数;
当x>2时f'(x)<0,故函数f(x)在(2,+∞)上为减函数,
故当x=2时函数f(x)有极大值f(2)=$\frac{3}{4}$+ln2;
(2)f′(x)=2a(x-1)+$\frac{1}{x}$,因函数f(x)在区间[2,4]上单调递减,
则f′(x)=2a(x-1)+$\frac{1}{x}$≤0在区间[2,4]上恒成立,
即2a≤$\frac{1}{{-x}^{2}+x}$在[2,4]上恒成立,
而当2≤x≤4时,$\frac{1}{{-x}^{2}+x}$∈[-$\frac{1}{2}$,-$\frac{1}{12}$],
2a≤-$\frac{1}{2}$,即a≤-$\frac{1}{4}$,故实数a的取值范围是(-∞,-$\frac{1}{4}$];
(3)因f(x)图象上的点都在 $\left\{\begin{array}{l}{x≥1}\\{y-x≤0}\end{array}\right.$所表示的平面区域内,
即当x∈[1,+∞)时,不等式f(x)≤x恒成立,
即a(x-1)2+lnx-x+1≤0恒成立,
设g(x)=a(x-1)2+lnx-x+1(x≥1),
只需g(x)max≤0即可,
由g′(x)=2a(x-1)+$\frac{1}{x}$-1=$\frac{2{ax}^{2}-(2a+1)x+1}{x}$,
(i)当a=0时,g′(x)=$\frac{1-x}{x}$,
当x>1时,g'(x)<0,
函数g(x)在(1,+∞)上单调递减,
故g(x)≤g(1)=0成立.
(ii)当a>0时,由g′(x)=$\frac{2a(x-1)(x-\frac{1}{2a})}{x}$,
令g'(x)=0,得x1=1或x2=$\frac{1}{2a}$,
①若$\frac{1}{2a}$≤1,即a≥$\frac{1}{2}$时,在区间[1,+∞)上,g'(x)≥0,
函数g(x)在[1,+∞)上单调递增,
函数g(x)在[1,+∞)上无最大值,不满足条件;
②若$\frac{1}{2a}$<1,即0<a<$\frac{1}{2}$时,
函数g(x)在[1,$\frac{1}{2a}$)上单调递减,在区间[$\frac{1}{2a}$,+∞)上单调递增,
同样g(x)在[1,+∞)无最大值,不满足条件.
(iii)当a<0时,因x∈[1,+∞),故g'(x)≤0,
则函数g(x)在[1,+∞)上单调递减,
故g(x)≤g(1)=0成立.
综上所述,实数a的取值范围是(-∞,0].
点评 本题考查考查函数的导数的应用,函数的极值,函数的单调性的应用,考查分析问题解决问题的能力.


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
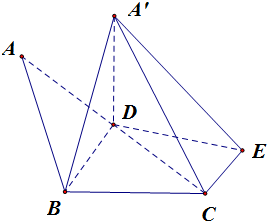 在△ABC中,AB=4,AC=4$\sqrt{2}$,∠BAC=45°,以AC的中线BD为折痕,将△ABD沿BD折起,如图所示,构成二面角A′-BD-C,在面BCD内作CE⊥CD,且$CE=\sqrt{2}$.
在△ABC中,AB=4,AC=4$\sqrt{2}$,∠BAC=45°,以AC的中线BD为折痕,将△ABD沿BD折起,如图所示,构成二面角A′-BD-C,在面BCD内作CE⊥CD,且$CE=\sqrt{2}$. 查看答案和解析>>
科目:高中数学 来源: 题型:解答题
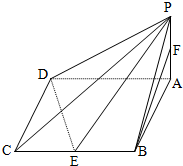 如图,四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD=60°,PA⊥平面ABCD,且PA=1,E,F分别是BC,PA的中点.
如图,四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD=60°,PA⊥平面ABCD,且PA=1,E,F分别是BC,PA的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 小明到他父亲的木工房,看到一个棱长为50cm的立方体工件(如图),从立方体的前后、左右、上下看,都有且仅有两个相通的正方形孔,请你算一算,这个立方体剩下的体积是多少?
小明到他父亲的木工房,看到一个棱长为50cm的立方体工件(如图),从立方体的前后、左右、上下看,都有且仅有两个相通的正方形孔,请你算一算,这个立方体剩下的体积是多少?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 优秀 | 非优秀 | 合计 | |
| 甲班 | 10 | 50 | 60 |
| 乙班 | 20 | 30 | 50 |
| 合计 | 30 | 80 | 110 |
| K2≥k | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| k | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |
| A. | 90% | B. | 95% | C. | 99% | D. | 99.9% |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com