
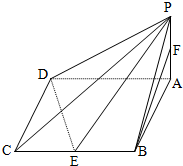
 如图,四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD=60°,PA⊥平面ABCD,且PA=1,E,F分别是BC,PA的中点.
如图,四棱锥P-ABCD的底面是边长为2的菱形,且∠BAD=60°,PA⊥平面ABCD,且PA=1,E,F分别是BC,PA的中点.分析 (Ⅰ)取AD的中点为G,连结BG,则BG∥ED,从而BG∥平面PDE,再由中位线定理得FG∥PD,从而FG∥平面PDE,进而平面BFG∥平面PDE,由此能证明BF∥平面PED.
(Ⅱ)推导出DE⊥BC,DE⊥AD,DE⊥PD,从而∠PDA是二面角P-DE-A的平面角,由此能求出二面角P-DE-A的大小.
(Ⅲ)点C到平面PDE的距离等于点B、点G到平面PDE的距离,过点G作GH垂直于PD,且与PD交于点H,GH的长为点C到平面PED的距离,由此能求出点C到平面PED的距离.
解答 证明:(Ⅰ)取AD的中点为G,连结BG,则BG∥ED,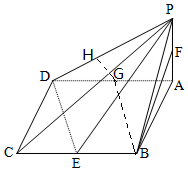
∴BG∥平面PDE,
△PAD中,F、G分别为所在边的中点,∴FG∥PD,
∴FG∥平面PDE,
∴平面BFG∥平面PDE,∴BF∥平面PED.
解:(Ⅱ)∵菱形ABCD,∠BAD=60°,
∴△BCD是正三角形,E是BC中点,∴DE⊥BC,
∴DE⊥AD,
又∵PA⊥平面ABCD,∴DE⊥PD,
∴∠PDA是二面角P-DE-A的平面角,
在Rt△PAD中,tan∠PDA=$\frac{1}{2}$,
∴二面角P-DE-A的大小为arctan$\frac{1}{2}$.
(Ⅲ)∵BE=CE,BG∥平面PDE,
∴点C到平面PDE的距离等于点B、点G到平面PDE的距离,
过点G作GH垂直于PD,且与PD交于点H,
∵DE⊥AD,DE⊥PD,∴DE⊥平面PAD,∴DE⊥GH,
∴GH⊥平面PDE,
∴GH的长为点C到平面PED的距离,
△PDA中,GH=$\frac{1}{2}×\frac{1×2}{\sqrt{1+{2}^{2}}}$=$\frac{\sqrt{5}}{5}$,
∴点C到平面PED的距离为$\frac{\sqrt{5}}{5}$.
点评 本题考查线面平行的证明,考查二面角的大小的求法,考查点到平面的距离的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某地为了改善居民的居住环境,争创国家卫生城市,在市民意见网站发布一项调查,每个住户在调研所居住的环境卫生后进行自主打分,最高分是10分.上个月该网站共有100个住户进行了打分,所有住户打分的平均分作为居民对该城市卫生现状满意度的参考分值,将这些打分结果分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到的频率分布直方图如图所示.
某地为了改善居民的居住环境,争创国家卫生城市,在市民意见网站发布一项调查,每个住户在调研所居住的环境卫生后进行自主打分,最高分是10分.上个月该网站共有100个住户进行了打分,所有住户打分的平均分作为居民对该城市卫生现状满意度的参考分值,将这些打分结果分成以下几组:第一组[0,2),第二组[2,4),第三组[4,6),第四组[6,8),第五组[8,10],得到的频率分布直方图如图所示.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 必定只有三点共线 | B. | 必有三点不共线 | ||
| C. | 至少有三点共线 | D. | 不可能有三点共线 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com