
 ij��Ϊ�˸��ƾ���ľ�ס���������������������У������������վ����һ����飬ÿ��ס���ڵ�������ס�Ļ������������������֣���߷���10�֣��ϸ��¸���վ����100��ס�������˴�֣�����ס����ֵ�ƽ������Ϊ����Ըó���������״����ȵIJο���ֵ������Щ��ֽ���ֳ����¼��飺��һ��[0��2�����ڶ���[2��4����������[4��6����������[6��8����������[8��10]���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ��
ij��Ϊ�˸��ƾ���ľ�ס���������������������У������������վ����һ����飬ÿ��ס���ڵ�������ס�Ļ������������������֣���߷���10�֣��ϸ��¸���վ����100��ס�������˴�֣�����ס����ֵ�ƽ������Ϊ����Ըó���������״����ȵIJο���ֵ������Щ��ֽ���ֳ����¼��飺��һ��[0��2�����ڶ���[2��4����������[4��6����������[6��8����������[8��10]���õ���Ƶ�ʷֲ�ֱ��ͼ��ͼ��ʾ������ ��1����Ƶ�ʷֲ�ֱ��ͼ������������ġ������Ƶ�ʣ�
��2���ٸ���վ�ڴ�ֽ���ϸߵĵ������ġ��������÷ֲ�����ķ�����ȡ6��ס�����������3�ˣ��ɵ����鹲��100��0.3=30��ס������ס������ס�����ڵ����飬������ס���ͬʱ��ѡ�еĸ��ʣ�
�ڵ���������X��ס����ѡ�У��������X�Ŀ���ȡֵΪ0��1��2���ֱ������Ӧ�ĸ��ʣ��ɴ������X�ķֲ��к���ѧ������
��� �⣺��1����Ƶ�ʷֲ�ֱ��ͼ�õ������Ƶ��Ϊ��0.150��2=0.3��
�������Ƶ��Ϊ��0.1��2=0.2��
�������Ƶ��Ϊ��0.05��2=0.1��
��2���ٸ���վ�ڴ�ֽ���ϸߵĵ������ġ��������÷ֲ�����ķ�����ȡ6��ס����
�������飺6��$\frac{0.3}{0.3+0.2+0.1}$=3�ˣ�
������飺6��$\frac{0.2}{0.3+0.2+0.1}$=2�ˣ�
������飺6��$\frac{0.1}{0.3+0.2+0.1}$=1�ˣ�
�ߵ����鹲��100��0.3=30��ס������ס������ס�����ڵ����飬
��ס���ͬʱ��ѡ�еĸ���p=$\frac{{C}_{2}^{2}{C}_{28}^{1}}{{C}_{30}^{3}}$=$\frac{1}{145}$��
�ڵ���������X��ס����ѡ�У��������X�Ŀ���ȡֵΪ0��1��2��
P��X=0��=$\frac{{C}_{3}^{1}+{C}_{3}^{2}}{{C}_{6}^{2}}$=$\frac{6}{15}$��
P��X=1��=$\frac{{C}_{3}^{1}{C}_{2}^{1}+{C}_{2}^{1}}{{C}_{6}^{2}}$=$\frac{8}{15}$��
P��X=2��=$\frac{{C}_{2}^{2}}{{C}_{6}^{2}}$=$\frac{1}{15}$��
��X�ķֲ���Ϊ��
| X | 0 | 1 | 2 |
| P | $\frac{6}{15}$ | $\frac{8}{15}$ | $\frac{1}{15}$ |
���� ���⿼����ʵ���������ɢ����������ķֲ��к���ѧ�����������е��⣬����ʱҪ�������⣬ע��Ƶ�ʷֲ�ֱ��ͼ�����ʵĺ������ã�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
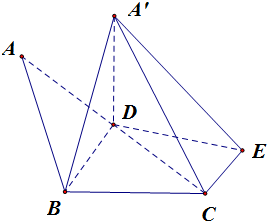 �ڡ�ABC�У�AB=4��AC=4$\sqrt{2}$����BAC=45�㣬��AC������BDΪ�ۺۣ�����ABD��BD������ͼ��ʾ�����ɶ����A��-BD-C������BCD����CE��CD����$CE=\sqrt{2}$��
�ڡ�ABC�У�AB=4��AC=4$\sqrt{2}$����BAC=45�㣬��AC������BDΪ�ۺۣ�����ABD��BD������ͼ��ʾ�����ɶ����A��-BD-C������BCD����CE��CD����$CE=\sqrt{2}$�� �鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
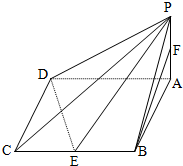 ��ͼ������P-ABCD�ĵ����DZ߳�Ϊ2�����Σ��ҡ�BAD=60�㣬PA��ƽ��ABCD����PA=1��E��F�ֱ���BC��PA���е㣮
��ͼ������P-ABCD�ĵ����DZ߳�Ϊ2�����Σ��ҡ�BAD=60�㣬PA��ƽ��ABCD����PA=1��E��F�ֱ���BC��PA���е㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 С����������ľ����������һ���ⳤΪ50cm�������幤������ͼ�������������ǰ�����ҡ����¿��������ҽ���������ͨ�������οף�������һ�㣬���������ʣ�µ�����Ƕ��٣�
С����������ľ����������һ���ⳤΪ50cm�������幤������ͼ�������������ǰ�����ҡ����¿��������ҽ���������ͨ�������οף�������һ�㣬���������ʣ�µ�����Ƕ��٣��鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com