
分析 (1)利用列举法求出从集合A,B中各任取一个数的基本事件15种,其中两数之和为0的有3种,由此能求出这两数之和为0的概率.
(2)基本事件共有15种,方程组$\left\{\begin{array}{l}ax+by=3\\ x+2y=2\end{array}\right.$只有一个解等价于两直线ax+by=3与x+2y=2只有一个交点,即b≠2a,利用列举法求出b=2a的事件有3种,由此能求出方程组$\left\{\begin{array}{l}ax+by=3\\ x+2y=2\end{array}\right.$只有一个解的概率.
解答 解:(1)由题意得,从集合A,B中各任取一个数的基本事件为:
(-1,-2),(-1,-1),(-1,0),(-1,1),(-1,2),
(0,-2),(0,-1),(0,0),(0,1),(0,2),
(1,-2),(1,-1),(1,0),(1,1),(1,2),
共有3×5=15(种),
其中两数之和为0的有(-1,1),(0,0),(1,-1)共3种,
故所求事件的概率为${P_1}=\frac{3}{15}=\frac{1}{5}$;
(2)由(1)基本事件共有15种,
又方程组$\left\{\begin{array}{l}ax+by=3\\ x+2y=2\end{array}\right.$只有一个解等价于两直线ax+by=3与x+2y=2只有一个交点,
所以$\frac{a}{1}≠\frac{b}{2}$,即b≠2a,而b=2a的事件有(-2,-1),(0,0),(2,1)共3种,
故所求事件的概率为${P_2}=1-\frac{3}{15}=\frac{4}{5}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法和对立事件概率计算公式的合理运用.


 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:解答题
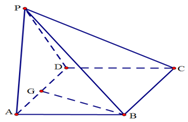 如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.
如图,四棱锥P-ABCD中,底面ABCD是∠DAB且边长为a的菱形,侧面PAD是等边三角形,且平面PAD⊥底面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的s-t图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )
甲、乙、丙.丁四辆玩具赛车同时从起点出发并做匀速直线运动,丙车最先到达终点.丁车最后到达终点.若甲、乙两车的s-t图象如图所示,则对于丙、丁两车的图象所在区域,判断正确的是( )| A. | 丙在Ⅲ区域,丁在Ⅰ区域 | B. | 丙在Ⅰ区城,丁在Ⅲ区域 | ||
| C. | 丙在Ⅱ区域,丁在Ⅰ区域 | D. | 丙在Ⅲ区域,丁在Ⅱ区域 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{24}{25}$ | B. | $\frac{7}{25}$ | C. | $-\frac{12}{25}$ | D. | $-\frac{24}{25}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{14π}{6}+12$ | B. | $\frac{11π}{3}+4$ | C. | $\frac{11π}{6}+12$ | D. | $\frac{11π}{3}+12$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com