

| A. | i≤2012 | B. | i>2012 | C. | i≤1006 | D. | i>1006 |
分析 根据流程图写出每次循环i,S的值,结合程序功能是$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2012}$比较即可确定退出循环的条件,得到答案.
解答 解:根据流程图,可知
第1次循环:i=2,S=$\frac{1}{2}$;
第2次循环:i=4,S=$\frac{1}{2}$+$\frac{1}{4}$;
第3次循环:i=6,S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$;
…
第1006次循环:i=2012,S=$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{6}$+…+$\frac{1}{2012}$;
此时,应退出循环,输出S的值.
故判断框内可填入i≤2012.
故选:A
点评 本题主要考察程序框图和算法,属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
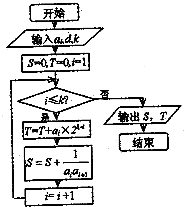 如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)
如图所示,流程图给出了无穷等差整数列{an}满足的条件,a1∈N+,且当k=5时,输出的S=-$\frac{5}{9}$,当k=10时,输出的S=-$\frac{10}{99}$.(其中d为公差)查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-3,0) | B. | (-3,-1] | C. | (-3,-1) | D. | (-3,3) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com