
分析 (Ⅰ)根据椭圆的离心率和焦距即可求出标准方程;
(Ⅱ)设过焦点F1的直线为l,分两类,若l的斜率不存在,求出答案,若l的斜率存在,不妨设为k,则l的方程为y=kx+1,根据韦达定理,弦长公式,点到直线的距离公式,得到S△2=6(1-$\frac{1}{m}$)2(1-$\frac{1}{{m}^{2}}$),构造函数f(t)=6(1-t)2(1-t2),利用导数求出函数的最值,问题得以解决.
解答 解:(Ⅰ)设椭圆的半焦距为c,则c=1,
又e=$\frac{c}{a}$=$\frac{\sqrt{3}}{3}$,可解得a=$\sqrt{3}$,
∴b2=a2-c2=2,
∴椭圆的标准方程为$\frac{{y}^{2}}{3}$+$\frac{{x}^{2}}{2}$=1;
(Ⅱ)设过焦点F1的直线为l,
①若l的斜率不存在,则A(0,$-\sqrt{3}$),B(0,$\sqrt{3}$),即|AB|=2$\sqrt{3}$,
显然当N在短轴顶点(0,$\sqrt{2}$)或(0,-$\sqrt{2}$)时,△NAB的面积最大,
此时,△NAB的最大面积为$\frac{1}{2}$×2$\sqrt{3}$×$\sqrt{2}$=$\sqrt{6}$.
②若l的斜率存在,不妨设为k,则l的方程为y=kx+1,
设A(x1,y1),B(x2,y2),
联立方程:$\left\{\begin{array}{l}{y=kx+1}\\{\frac{{y}^{2}}{3}+\frac{{x}^{2}}{2}=1}\end{array}\right.$,消去y整理得:(2k2+3)x2+4kx-4=0,
∴x1+x2=-$\frac{4k}{2{k}^{2}+3}$,x1x2=-$\frac{4}{2{k}^{2}+3}$,
则|AB|=$\sqrt{1+{k}^{2}}$|x1-x2|=$\frac{4\sqrt{3}({k}^{2}+1)}{2{k}^{2}+3}$,
∵当直线与l平行且与椭圆相切时,此时切点N到直线l的距离最大,
设切线l′:y=kx+m,(m≤-$\sqrt{2}$),
联立方程:$\left\{\begin{array}{l}{y=kx+m}\\{\frac{{y}^{2}}{3}+\frac{{x}^{2}}{2}=1}\end{array}\right.$,消去x整理得:(2k2+3)y2+4kmy+2m2-6=0,
由△=(4km)2-4(2k2+3)(2m2-6)=0,
解得m2=2k2+3,(m<-$\sqrt{3}$),
又点N到直线l的距离d=$\frac{|m-1|}{\sqrt{{k}^{2}+1}}$,
∴S△=$\frac{1}{2}$d|AB|=$\frac{1}{2}$×$\frac{|m-1|}{\sqrt{{k}^{2}+1}}$$\frac{4\sqrt{3}({k}^{2}+1)}{2{k}^{2}+3}$,
∴S△2=$\frac{12(m-1)^{2}({k}^{2}+1)}{(2{k}^{2}+3)^{2}}$=6(1-$\frac{1}{m}$)2(1-$\frac{1}{{m}^{2}}$),
令t=$\frac{1}{m}$(-$\frac{\sqrt{3}}{3}$,0)
设f(t)=6(1-t)2(1-t2),
∴f′(t)=12(1-t)2(2t+1),
∵当t∈(-$\frac{\sqrt{3}}{3}$,-$\frac{1}{2}$)时,f′(t)>0,当t∈(-$\frac{1}{2}$,0)时,f′(t)<0,
∴f(t)在(-$\frac{\sqrt{3}}{3}$,-$\frac{1}{2}$)上是增函数,在(-$\frac{1}{2}$,0)为减函数,
∴f(t)min=f(-$\frac{1}{2}$)=$\frac{81}{8}$,
故k2=$\frac{1}{2}$时,△NAB的最大面积为$\frac{9\sqrt{2}}{4}$,
显然$\sqrt{6}$<$\frac{9\sqrt{2}}{4}$,
∴当l的方程为y=±$\frac{\sqrt{2}}{2}$x+1,△NAB的面积最大,最大值为$\frac{9\sqrt{2}}{4}$.
点评 本题主要考查椭圆的标准方程、直线与圆锥曲线的位置关系,利用导数求函数的最值问题,考查运算能力,考查化归思想,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 6 | B. | 4$\sqrt{2}$ | C. | 3+2$\sqrt{2}$ | D. | 3+4$\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
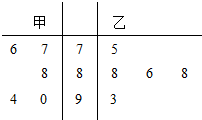 在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )
在“唱响内江”选拔赛中,甲、乙两位歌手的5次得分情况如茎叶图所示,记甲、乙两人的平均得分分别$\overline{{X}_{甲}}$、$\overline{{X}_{乙}}$,则下列判断正确的是( )| A. | $\overline{{X}_{甲}}$<$\overline{{X}_{乙}}$,乙比甲成绩稳定 | B. | $\overline{{X}_{甲}}$<$\overline{{X}_{乙}}$,甲比乙成绩稳定 | ||
| C. | $\overline{{X}_{甲}}$>$\overline{{X}_{乙}}$,甲比乙成绩稳定 | D. | $\overline{{X}_{甲}}$>$\overline{{X}_{乙}}$,乙比甲成绩稳定 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{3}}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com