
ЎҫМвДҝЎҝДі№«ЛҫјЖ»®Н¶ЧКAЎўBБҪЦЦҪрИЪІъЖ·Ј¬ёщҫЭКРіЎөчІйУлФӨІвЈ¬AІъЖ·өДАыИуУлН¶ЧКБҝіЙХэұИАэЈ¬Жд№ШПөИзНј1Ј¬BІъЖ·өДАыИуУлН¶ЧКБҝөДЛгКхЖҪ·ҪёщіЙХэұИАэЈ¬Жд№ШПөИзНј2(ЧўЈәАыИуУлН¶ЧКБҝөДөҘО»ЈәНтФӘ)Ј®
(1)·ЦұрҪ«AЎўBБҪІъЖ·өДАыИуұнКҫОӘН¶ЧКБҝөДәҜКэ№ШПөКҪЈ»
(2)ёГ№«ЛҫТСУР10НтФӘЧКҪрЈ¬ІўИ«ІҝН¶ИлAЎўBБҪЦЦІъЖ·ЦРЈ¬ОКЈәФхСщ·ЦЕдХв10НтФӘН¶ЧКЈ¬ІЕДЬК№№«Лҫ»сөГЧоҙуАыИуЈҝЖдЧоҙуАыИуОӘ¶аЙЩНтФӘЈҝ

Ўҫҙр°ёЎҝЈЁ1Ј©јыҪвОцЈ»ЈЁ2Ј©2.8НтФӘ
ЎҫҪвОцЎҝ
КФМв·ЦОцЈәЈЁ1Ј©УЙУЪAІъЖ·өДАыИуyУлН¶ЧКБҝxіЙХэұИАэЈ¬BІъЖ·өДАыИуyУлН¶ЧКБҝxөДЛгКхЖҪ·ҪёщіЙХэұИАэЈ¬№КҝЙЙиәҜКэ№ШПөКҪЈ¬АыУГНјПуЦРөДМШКвөгЈ¬ҝЙЗуәҜКэҪвОцКҪЈ»
ЈЁ2Ј©ЙиAІъЖ·Н¶ИлxНтФӘЈ¬ФтBІъЖ·Н¶Ил10©ҒxНтФӘЈ¬ЙиЖуТөАыИуОӘyНтФӘЈ®АыУГЈЁ1Ј©УЙҙЛҝЙҪЁБўәҜКэЈ¬ІЙУГ»»ФӘ·ЁЈ¬ЧӘ»ҜОӘ¶юҙОәҜКэЈ®АыУГЕд·Ҫ·ЁЗуәҜКэөДЧоЦөЈ®
ҪвЈәЈЁ1Ј©ЙиН¶ЧКОӘxНтФӘЈ¬AІъЖ·өДАыИуОӘfЈЁxЈ©НтФӘЈ¬BІъЖ·өДАыИуОӘgЈЁxЈ©НтФӘЈ®
УЙМвТвЙиfЈЁxЈ©=k1xЈ¬![]() Ј®УЙНјЦӘ
Ј®УЙНјЦӘ![]() Ј¬Ўа
Ј¬Ўа![]()
УЦgЈЁ4Ј©=1.6Ј¬Ўа![]() Ј®ҙУ¶ш
Ј®ҙУ¶ш![]() Ј¬
Ј¬![]()
ЈЁ2Ј©ЙиAІъЖ·Н¶ИлxНтФӘЈ¬ФтBІъЖ·Н¶Ил10©ҒxНтФӘЈ¬ЙиЖуТөАыИуОӘyНтФӘЈ®
![]() ЈЁ0ЎЬxЎЬ10Ј©
ЈЁ0ЎЬxЎЬ10Ј©
Бо![]() Ј¬Фт
Ј¬Фт![]() =
=![]()
![]()
өұt=2КұЈ¬![]() Ј¬ҙЛКұx=10©Ғ4=6
Ј¬ҙЛКұx=10©Ғ4=6
ҙрЈәөұAІъЖ·Н¶Ил6НтФӘЈ¬ФтBІъЖ·Н¶Ил4НтФӘКұЈ¬
ёГЖуТө»сөГЧоҙуАыИуЈ¬АыИуОӘ2.8НтФӘЈ®



| Дкј¶ | ёЯЦРҝОіМ | Дкј¶ | іхЦРҝОіМ |
| ёЯТ» | ёЯТ»Гв·СҝОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СҝОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СҝОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СҝОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СҝОіМНЖјцЈЎ | іхИэ | іхИэГв·СҝОіМНЖјцЈЎ |
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘПВБРЛДёцГьМв:
ўЩәҜКэ![]() ВъЧг:¶ФИОТв
ВъЧг:¶ФИОТв![]() УР
УР![]() Ј»
Ј»
ўЪәҜКэ![]() ҫщОӘЖжәҜКэЈ»
ҫщОӘЖжәҜКэЈ»
ўЫИфәҜКэ![]() ФЪ
ФЪ![]() ЙПУРТвТеЈ¬Фт
ЙПУРТвТеЈ¬Фт![]() өДИЎЦө·¶О§КЗ
өДИЎЦө·¶О§КЗ![]() Ј»
Ј»
ўЬЙи![]() КЗ№ШУЪ
КЗ№ШУЪ![]() өД·ҪіМ
өД·ҪіМ![]() ,(
,(![]() ЗТ
ЗТ![]() )өДБҪёщ,Фт
)өДБҪёщ,Фт![]() ;
;
ЖдЦРХэИ·ГьМвөДРтәЕКЗ__________Ј®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝИзНјЛщКҫЈ¬ИэАвЦщABC©ҒA1B1C1ЦРЈ¬ІаАвAA1ЎНөЧГжA1B1C1Ј¬AA1ЈҪ1Ј¬өЧГжИэҪЗРОA1B1C1КЗұЯіӨОӘ2өДХэИэҪЗРОЈ¬EКЗBCЦРөгЈ¬ФтПВБРЛө·ЁХэИ·өДКЗЈЁ Ј©

ўЩCC1УлAB1ЛщіЙҪЗөДУаПТЦөОӘ![]()
ўЪABЎНЖҪГжACC1A1
ўЫИэҪЗРОAB1EОӘЦұҪЗИэҪЗРО
ўЬA1C1ЎОЖҪГжAB1E
A.ўЩўЪB.ўЫўЬC.ўЩўЫD.ўЪўЬ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
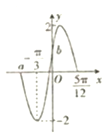
ЎҫМвДҝЎҝәҜКэfЈЁxЈ©=AsinЈЁ2ҰШx+ҰХЈ©ЈЁAЈҫ0Ј¬ҰШЈҫ0Ј¬|ҰХ|Јј![]() Ј©өДІҝ·ЦНјПуИзНјЛщКҫ
Ј©өДІҝ·ЦНјПуИзНјЛщКҫ
ЈЁ1Ј©ЗуAЈ¬ҰШЈ¬ҰХөДЦөЈ»
ЈЁ2Ј©ЗуНјЦРaЈ¬bөДЦөј°әҜКэfЈЁxЈ©өДөЭФцЗшјдЈ»
ЈЁ3Ј©ИфҰБЎК[0Ј¬ҰР]Ј¬ЗТfЈЁҰБЈ©=![]() Ј¬ЗуҰБөДЦөЈ®
Ј¬ЗуҰБөДЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТ»ёцФІЧ¶өЧГж°лҫ¶ОӘ![]() Ј¬ёЯОӘ
Ј¬ёЯОӘ![]() Ј¬
Ј¬
ЈЁ1Ј©ЗуФІЧ¶өДұнГж»э.
ЈЁ2Ј©ЗуФІЧ¶өДДЪҪУХэЛДАвЦщұнГж»эөДЧоҙуЦөЈ®
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝТСЦӘәҜКэ![]() ¶ЁТеФЪ
¶ЁТеФЪ![]() ЙПЗТВъЧгПВБРБҪёцМхјю:
ЙПЗТВъЧгПВБРБҪёцМхјю:
ўЩ¶ФИОТв![]() ¶јУР
¶јУР![]() ;
;
ўЪөұ![]() Кұ,УР
Кұ,УР![]() Ј¬
Ј¬
ЈЁ1Ј©Зу![]() Ј¬ІўЦӨГчәҜКэ
Ј¬ІўЦӨГчәҜКэ![]() ФЪ
ФЪ![]() ЙПКЗЖжәҜКэЈ»
ЙПКЗЖжәҜКэЈ»
ЈЁ2Ј©СйЦӨәҜКэ![]() КЗ·сВъЧгХвР©МхјюЈ»
КЗ·сВъЧгХвР©МхјюЈ»
ЈЁ3Ј©Иф![]() Ј¬КФЗуәҜКэ
Ј¬КФЗуәҜКэ![]() өДБгөг.
өДБгөг.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ5ГыДРЙъ3ГыЕ®ЙъІОјУЙэЖмТЗКҪЈә
ЈЁ1Ј©ХҫБҪәбЕЕЈ¬3ГыЕ®ЙъХҫЗ°ЕЕЈ¬5ГыДРЙъХҫәуЕЕУР¶аЙЩЦЦХҫ·ЁЈҝ
ЈЁ2Ј©ХҫБҪЧЭБРЈ¬ГҝБР4ИЛЈ¬ГҝБР¶јУРЕ®ЙъЗТЕ®ЙъХҫФЪДРЙъЗ°ГжЈ¬УР¶аЙЩЦЦЕЕБР·Ҫ·ЁЈҝ
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝ№юКҰҙуёҪЦРёЯИэС§ДкНіјЖјЧЎўТТБҪёц°ај¶Т»ДЈКэС§·ЦКэ(Въ·Ц150·Ц),Гҝёц°ај¶20ГыН¬С§,ПЦУРјЧЎўТТБҪО»Н¬С§өД20ҙОіЙјЁИзПВБРҫҘТ¶НјЛщКҫ:

(I)ёщҫЭ»щТ¶НјЗујЧЎўТТБҪО»Н¬С§іЙјЁөДЦРО»Кэ,ІўҪ«ТТН¬С§өДіЙјЁөДЖөВК·ЦІјЦұ·ҪНјМоідНкХыЈ»

(ўт)ёщҫЭ»щТ¶НјұИҪПјЧТТБҪО»Н¬С§КэС§іЙјЁөДЖҪҫщЦөј°ОИ¶ЁіМ¶И(І»ТӘЗујЖЛгіцҫЯМеЦөЈ¬ёшіцҪбВЫјҙҝЙ)
(ўу)ПЦҙУјЧТТБҪО»Н¬С§өДІ»өНУЪ140·ЦөДіЙјЁЦРИОТвСЎіц2ёціЙјЁЈ¬ЙиКВјю![]() ОӘЎ°ЖдЦР2 ёціЙјЁ·ЦұрКфУЪІ»Н¬өДН¬С§ЎұЈ¬ЗуКВјю
ОӘЎ°ЖдЦР2 ёціЙјЁ·ЦұрКфУЪІ»Н¬өДН¬С§ЎұЈ¬ЗуКВјю![]() ·ўЙъөДёЕВК.
·ўЙъөДёЕВК.
Ійҝҙҙр°ёәНҪвОц>>
ҝЖДҝЈәёЯЦРКэС§ АҙФҙЈә МвРНЈә
ЎҫМвДҝЎҝјЧТТБҪёц°ај¶ҫщОӘ40ИЛЈ¬ҪшРРТ»ГЕҝјКФәуЈ¬°ҙС§ЙъҝјКФіЙјЁј°ёсУлІ»ј°ёсҪшРРНіјЖЈ¬јЧ°ај°ёсИЛКэОӘ36ИЛЈ¬ТТ°ај°ёсИЛКэОӘ24ИЛЈ®
ЈЁ1Ј©ёщҫЭТФЙПКэҫЭҪЁБўТ»ёц2ЎБ2өДБРБӘұнЈ»
ЈЁ2Ј©КФЕР¶ПДЬ·сУР99.5%өД°СОХИПОӘЎ°ҝјКФіЙјЁУл°ај¶УР№ШЎұЈҝІОҝј№«КҪЈә![]()
![]() Ј»nЈҪa+b+c+d
Ј»nЈҪa+b+c+d
PЈЁ | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
Ійҝҙҙр°ёәНҪвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБРұн - КФМвБРұн
әюұұКЎ»ҘБӘНшОҘ·ЁәНІ»БјРЕПўҫЩұЁЖҪМЁ | НшЙПУРәҰРЕПўҫЩұЁЧЁЗш | өзРЕХ©ЖӯҫЩұЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРәҰРЕПўҫЩұЁЧЁЗш | ЙжЖуЗЦИЁҫЩұЁЧЁЗш
ОҘ·ЁәНІ»БјРЕПўҫЩұЁөз»°Јә027-86699610 ҫЩұЁУКПдЈә58377363@163.com