
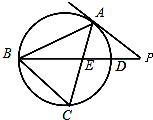
 解:∵PB=PD+BD=1+8=9,
解:∵PB=PD+BD=1+8=9,| 7 |
| 7 |
| 7 |


科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| sinα+cosα |
| sinα-cosα |
| 3 |
| 2 |
cos(α-
| ||
sin(
|
查看答案和解析>>
科目:高中数学 来源: 题型:
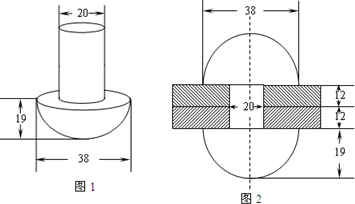 如图,在两块钢板上打孔,用顶帽呈半球形,钉身为圆柱形的铆钉(图1)穿在一起,在没有帽的一段每打出一个帽,使得与顶帽的大小相等,铆合的两块钢板,成为某种钢结构的配件,其截面图如图2(单位:mm)(加工中不计损失).
如图,在两块钢板上打孔,用顶帽呈半球形,钉身为圆柱形的铆钉(图1)穿在一起,在没有帽的一段每打出一个帽,使得与顶帽的大小相等,铆合的两块钢板,成为某种钢结构的配件,其截面图如图2(单位:mm)(加工中不计损失).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com